题目内容
 如图:一个圆锥的母线为20cm,底面半径为5cm,有一甲虫从底面A点出发沿侧面爬行一周后返回A点,则甲虫爬行的最短距离是
如图:一个圆锥的母线为20cm,底面半径为5cm,有一甲虫从底面A点出发沿侧面爬行一周后返回A点,则甲虫爬行的最短距离是考点:平面展开-最短路径问题,圆锥的计算
专题:
分析:易得圆锥的底面周长也就是圆锥的侧面展开图的弧长,利用弧长公式即可求得侧面展开图的圆心角,进而构造直角三角形求得相应线段即可.
解答:
 解:圆锥的底面周长=2π×5=10π(cm),
解:圆锥的底面周长=2π×5=10π(cm),
设侧面展开图的圆心角的度数为n.
∴
=10π,
解得:n=90,
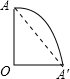
圆锥的侧面展开图,如图所示:
∴最短路程为:
=20
(cm),
故答案为:20
cm.

 解:圆锥的底面周长=2π×5=10π(cm),
解:圆锥的底面周长=2π×5=10π(cm),设侧面展开图的圆心角的度数为n.
∴
| nπ×20 |
| 180 |
解得:n=90,
圆锥的侧面展开图,如图所示:
∴最短路程为:
| 202+202 |
| 2 |
故答案为:20
| 2 |
点评:此题主要考查了平面展开最短路径以及圆锥有关计算,求立体图形中两点之间的最短路线长,一般应放在平面内,构造直角三角形,求两点之间的线段的长度.用到的知识点为:圆锥的弧长等于底面周长.

练习册系列答案
相关题目

 如图,A、B、C三点在正方形网格线的交点处,若将△ABC绕着点A逆时针旋转得到△AB1C1,则tanB1的值为
如图,A、B、C三点在正方形网格线的交点处,若将△ABC绕着点A逆时针旋转得到△AB1C1,则tanB1的值为 如图,已知二次函数y=x2+bx+c的图象的对称轴为过点(1,0)且与y轴平行的直线,点A、B均在图象上,且直线AB与x轴平行,若点A的坐标为(0,
如图,已知二次函数y=x2+bx+c的图象的对称轴为过点(1,0)且与y轴平行的直线,点A、B均在图象上,且直线AB与x轴平行,若点A的坐标为(0, 如图,在四边形ABCD中,若AD∥BC,BC=CD=AC=6,AB=3
如图,在四边形ABCD中,若AD∥BC,BC=CD=AC=6,AB=3 如图,在?ABCD中,∠B=80°,∠ADC的角平分线DE与BC交于点E.若BE=CE,则∠DAE=
如图,在?ABCD中,∠B=80°,∠ADC的角平分线DE与BC交于点E.若BE=CE,则∠DAE= 如图,⊙0的半径OD上弦AB于点C,若AB=8,CD=2,则⊙0的半径为
如图,⊙0的半径OD上弦AB于点C,若AB=8,CD=2,则⊙0的半径为