题目内容
某物流公司的快递车和货车每天往返于甲、乙两地,快递车比货车多往返一趟.已知货车比快递车早1小时出发,到达乙地后用1小时装卸货物,然后按原路以原速返回,结果与第二趟返回的快递车同时到达甲地.下图表示快递车距离甲地的路程y(km)与货车出发所用时间x(h)之间的函数关系图象.
(1)①请在下图中画出货车距离甲地的路程y(km)与所用时间x( h)的函数关系图象;②两车在中途相遇 次.
(2)试求货车从乙地返回甲地时y(km)与所用时间x( h)的函数关系式.
(3)求快递车第二次从甲地出发到与返程货车相遇所用时间为多少h?这时货车离乙地多少km?

(1)①请在下图中画出货车距离甲地的路程y(km)与所用时间x( h)的函数关系图象;②两车在中途相遇
(2)试求货车从乙地返回甲地时y(km)与所用时间x( h)的函数关系式.
(3)求快递车第二次从甲地出发到与返程货车相遇所用时间为多少h?这时货车离乙地多少km?

考点:一次函数的应用
专题:
分析:(1)求出货车从甲地开往乙地的时间,然后作出函数图象,再根据图象判断出相遇的次数即可;
(2)设y=kx+b(k≠0),然后利用待定系数法求一次函数解析式解答;
(3)求出快递车第二次从甲地出发的函数解析式,在与货车的解析式联立求解得到距离乙地的距离,然后求解即可.
(2)设y=kx+b(k≠0),然后利用待定系数法求一次函数解析式解答;
(3)求出快递车第二次从甲地出发的函数解析式,在与货车的解析式联立求解得到距离乙地的距离,然后求解即可.
解答: 解:(1)①由题意得,货车从甲地到达乙地的时间为
解:(1)①由题意得,货车从甲地到达乙地的时间为
×(9-1)=4小时,
所以,从4小时到5小时y=200km,9小时时y=0km,
作函数图象如图所示,
②两车在中途相遇3次;
(2)设y=kx+b(k≠0),
∵函数图象经过点(5,200),(9,0),
∴
,
解得
,
∴y=-50x+450;
(3)设快递车第二次从甲地出发的函数解析式为y=mx+n(m≠0),
则
,
解得
,
∴y=100x-500,
联立
,
解得
,
∴
-5=
小时,
200-
=
km,
答:快递车第二次从甲地出发到与返程货车相遇所用时间为
小时,这时货车离乙地
km.
 解:(1)①由题意得,货车从甲地到达乙地的时间为
解:(1)①由题意得,货车从甲地到达乙地的时间为| 1 |
| 2 |
所以,从4小时到5小时y=200km,9小时时y=0km,
作函数图象如图所示,
②两车在中途相遇3次;
(2)设y=kx+b(k≠0),
∵函数图象经过点(5,200),(9,0),
∴
|
解得
|
∴y=-50x+450;
(3)设快递车第二次从甲地出发的函数解析式为y=mx+n(m≠0),
则
|
解得
|
∴y=100x-500,
联立
|
解得
|
∴
| 19 |
| 3 |
| 4 |
| 3 |
200-
| 400 |
| 3 |
| 200 |
| 3 |
答:快递车第二次从甲地出发到与返程货车相遇所用时间为
| 4 |
| 3 |
| 200 |
| 3 |
点评:本题考查了一次函数的应用,主要利用了待定系数法求一次函数解析式,相遇问题,读懂题目信息,理解两车的运动过程是解题的关键.

练习册系列答案
相关题目
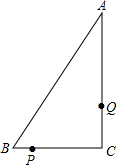 如图,在Rt△ABC中,∠C=90°,AC=8cm,BC=6CM.点P,Q同时由B,A两点出发,分别沿射线BC,AC方向以1cm/s的速度匀速运动.
如图,在Rt△ABC中,∠C=90°,AC=8cm,BC=6CM.点P,Q同时由B,A两点出发,分别沿射线BC,AC方向以1cm/s的速度匀速运动.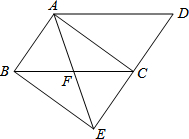 如图,将?ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
如图,将?ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F. 如图,以?ABCD的边AB为直径的⊙O经过点D,点E在⊙O上,∠AED=45°,
如图,以?ABCD的边AB为直径的⊙O经过点D,点E在⊙O上,∠AED=45°,
 如图:一个圆锥的母线为20cm,底面半径为5cm,有一甲虫从底面A点出发沿侧面爬行一周后返回A点,则甲虫爬行的最短距离是
如图:一个圆锥的母线为20cm,底面半径为5cm,有一甲虫从底面A点出发沿侧面爬行一周后返回A点,则甲虫爬行的最短距离是