题目内容
8.先化简:($\frac{a-2}{{a}^{2}+2a}$-$\frac{a-1}{{a}^{2}+4a+4}$)÷$\frac{a-4}{a+2}$,在4,-2,1,0中选择一个合适的值带入求值.分析 先根据分式混合运算的法则把原式进行化简,再选取合适的x的值代入进行计算即可.
解答 解:($\frac{a-2}{{a}^{2}+2a}$-$\frac{a-1}{{a}^{2}+4a+4}$)÷$\frac{a-4}{a+2}$
=($\frac{a-2}{{a}^{2}+2a}$-$\frac{a-1}{{a}^{2}+4a+4}$)÷$\frac{a-4}{a+2}$,
=$\frac{(a-2)(a+2)-a(a-1)}{a(a+2)^{2}}$×$\frac{a+2}{a-4}$
=$\frac{a-4}{a(a+2)^{2}}$×$\frac{a+2}{a-4}$
=$\frac{1}{a(a+2)}$,
当a=1时,原式=$\frac{1}{1×(1+2)}$=$\frac{1}{3}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
3. 如图,D是线段AB的中点,C是线段AB的垂直平分线上的一点,DE⊥AC于点E,DF⊥BC于点F.
如图,D是线段AB的中点,C是线段AB的垂直平分线上的一点,DE⊥AC于点E,DF⊥BC于点F.
(1)求证:DE=DF;
(2)当CD与AB满足怎样的数量关系时,四边形CEDF为正方形?请说明理由.
 如图,D是线段AB的中点,C是线段AB的垂直平分线上的一点,DE⊥AC于点E,DF⊥BC于点F.
如图,D是线段AB的中点,C是线段AB的垂直平分线上的一点,DE⊥AC于点E,DF⊥BC于点F.(1)求证:DE=DF;
(2)当CD与AB满足怎样的数量关系时,四边形CEDF为正方形?请说明理由.
20.一元二次方程5x2-7x+5=0的根的情况为( )
| A. | 有两个不相等的实数根 | B. | 没有实数根 | ||
| C. | 有两个相等的实数根 | D. | 只有一个实数根 |
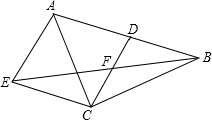 在△ABC中,CD是AB边上的中线,F是CD的中点,过点C作AB的平行线交BF的延长线于点E,连接AE
在△ABC中,CD是AB边上的中线,F是CD的中点,过点C作AB的平行线交BF的延长线于点E,连接AE