题目内容
19.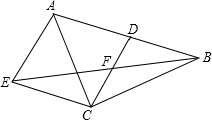 在△ABC中,CD是AB边上的中线,F是CD的中点,过点C作AB的平行线交BF的延长线于点E,连接AE
在△ABC中,CD是AB边上的中线,F是CD的中点,过点C作AB的平行线交BF的延长线于点E,连接AE(1)求证:EC=DA;
(2)填空:
①当AC⊥CB时,四边形AECD的形状是菱形;
②当AC=CB时,四边形AECD的形状是矩形.
分析 (1)根据平行线的性质得出∠FEC=∠DBF,∠ECF=∠BDF,F是CD的中点,得出FD=CF,再利用AAS证明△FEC与△FBD全等,进一步证明即可;
(2)利用直角三角形的性质:斜边上的中线等于斜边的一半,得出CD=DA,进一步得出结论即可;
(3)由等腰三角形的性质得出CD⊥AB,即可得出结论.
解答 (1)证明:∵EC∥AB,
∴∠FEC=∠DBF,∠ECF=∠BDF,
∵F是CD的中点,
∴FD=CF,
在△FEC与△FBD中,$\left\{\begin{array}{l}{∠FEC=∠DBF}&{\;}\\{∠ECF=∠BDF}&{\;}\\{FD=CF}&{\;}\end{array}\right.$,
∴△FEC≌△FBD(AAS),
∴EC=BD,
又∵CD是AB边上的中线,
∴BD=DA,
∴EC=DA.
(2)解:AC⊥CB时,四边形AECD是菱形;理由如下:
∵EC=AD,EC∥AD,
∴四边形AECD是平行四边形,
∵AC⊥CB,CD是AB边上的中线,
∴CD=AD=BD,
∴四边形AECD是菱形;故答案为:⊥.
(3)解:当AC=CB时,四边形AECD的是矩形;理由如下:
∵AB=AC,CD是AB边上的中线,
∴CD⊥AB,
∴∠ADC=90°,
又∵四边形AECD是平行四边形,
∴四边形AECD的是矩形;
故答案为:=.
点评 此题考查三角形全等的判定与性质,平行四边形的判定以及菱形的判定,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
10.下列式子成立的是( )
| A. | 2x-3x=-1 | B. | -3(a-1)=-3a-3 | C. | 2x•3x=6x | D. | 6a÷3a=2 |
7. 如图,在4×4正方形网格中,任选一个白色的小正方形并涂黑,使图中黑色部分的图形仍然构成一个轴对称图形的概率是( )
如图,在4×4正方形网格中,任选一个白色的小正方形并涂黑,使图中黑色部分的图形仍然构成一个轴对称图形的概率是( )
 如图,在4×4正方形网格中,任选一个白色的小正方形并涂黑,使图中黑色部分的图形仍然构成一个轴对称图形的概率是( )
如图,在4×4正方形网格中,任选一个白色的小正方形并涂黑,使图中黑色部分的图形仍然构成一个轴对称图形的概率是( )| A. | $\frac{6}{13}$ | B. | $\frac{5}{13}$ | C. | $\frac{4}{13}$ | D. | $\frac{3}{13}$ |
11.下列计算正确的是( )
| A. | 2-1=-2 | B. | 20=0 | C. | (a3)2=a6 | D. | 2a+3a=6a |
 如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF;②∠DAF=15°;③AC垂直平分EF;④BE+DF=EF;⑤S△CEF=S△ABE,其中正确的有①②③.
如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF;②∠DAF=15°;③AC垂直平分EF;④BE+DF=EF;⑤S△CEF=S△ABE,其中正确的有①②③. 如图,在△ABC中,∠C=90°,点E在AB上,以AE为直径的⊙O切BC于点D,连接AD.
如图,在△ABC中,∠C=90°,点E在AB上,以AE为直径的⊙O切BC于点D,连接AD.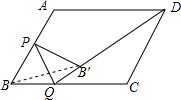 如图,菱形ABCD的边长为4,∠ABC=60°,点P是边AB的中点,点Q为边BC上的动点,联结PQ,作B关于PQ的对称点B′,则B′D长度的最小值是2$\sqrt{7}$-2.
如图,菱形ABCD的边长为4,∠ABC=60°,点P是边AB的中点,点Q为边BC上的动点,联结PQ,作B关于PQ的对称点B′,则B′D长度的最小值是2$\sqrt{7}$-2.