题目内容
已知不等式组
(其中a>b)共有2个整数解,设
=m,则m的取值范围是( )
|
| a2-b2 |
| ab |
| A、1<m<3 |
| B、-3<m<-1或1<m<3 |
| C、1≤m<3 |
| D、-3<m≤-1或1≤m<3 |
考点:一元一次不等式组的整数解
专题:计算题
分析:分类讨论:当a>b>0,解不等式组得
<x<
,由于0<
<1,而不等式组共有2个整数解,得到1<
≤3,变形m得到m=
-
,然后利用数轴中两点之间的距离得到1<m<3;当0>a>b,解不等式组得
<x<
<,由于1<
<2,而不等式组共有2个整数解,则3<
≤4,同样可得-3<m<-1;当a>0>b时,解不等式组得x>
,不能只含有有2个整数解,故舍去.
| b |
| a |
| a |
| b |
| b |
| a |
| a |
| b |
| a |
| b |
| b |
| a |
| a |
| b |
| b |
| a |
| a |
| b |
| a |
| b |
| b |
| a |
解答:解:当a>b>0,解不等式组得
<x<
,
∵0<
<1,而不等式组共有2个整数解,
∴1<
≤3,
∵m=
-
,
∴1<m<3;
当0>a>b,解不等式组得
<x<
<,
∵1<
<2,而不等式组共有2个整数解,
∴3<
≤4,
∵m=
-
,
∴-3<m<-1;
当a>0>b时,解不等式组得x>
,不能只含有有2个整数解,故舍去,
∴m的取值范围为-3<m<-1或1<m<3.
故选B.
| b |
| a |
| a |
| b |
∵0<
| b |
| a |
∴1<
| a |
| b |
∵m=
| a |
| b |
| b |
| a |
∴1<m<3;
当0>a>b,解不等式组得
| a |
| b |
| b |
| a |
∵1<
| a |
| b |
∴3<
| a |
| b |
∵m=
| a |
| b |
| b |
| a |
∴-3<m<-1;
当a>0>b时,解不等式组得x>
| b |
| a |
∴m的取值范围为-3<m<-1或1<m<3.
故选B.
点评:本题考查了一元一次不等式组的整数解:利用数轴确定不等式组的解(整数解).解决此类问题的关键在于正确解得不等式组或不等式的解集,然后再根据题目中对于解集的限制得到下一步所需要的条件,再根据得到的条件进而求得不等式组的整数解.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
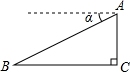 在寻找马航MH370航班过程中,某搜寻飞机在空中A处发现海面上一块疑似漂浮目标B,此时从飞机上看目标B的俯角为α,已知飞行高度AC=1500米,tanα=
在寻找马航MH370航班过程中,某搜寻飞机在空中A处发现海面上一块疑似漂浮目标B,此时从飞机上看目标B的俯角为α,已知飞行高度AC=1500米,tanα=
| ||
| 5 |
A、2400
| ||
B、2400
| ||
C、2500
| ||
D、2500
|
 如图,在平行四边形ABCD中,∠A=135°,E,F分别是边AB和BC的中点,EP⊥CD于点P,若AB=8,AD=3
如图,在平行四边形ABCD中,∠A=135°,E,F分别是边AB和BC的中点,EP⊥CD于点P,若AB=8,AD=3| 2 |
| A、4 | ||||
B、
| ||||
C、
| ||||
D、
|
分式
+
的化简结果为( )
| 1 |
| x |
| 1 |
| x(x-1) |
| A、x | ||
B、
| ||
C、
| ||
D、
|
计算2sin30°-cos245°的值是( )
| A、1 | B、-1 | C、0.5 | D、0 |
如果a、b是方程x2-3x+1=0的两根,那么代数式a2+2b2-3b的值为( )
| A、6 | B、-6 | C、7 | D、-7 |
 如图,在△ABC中,M、N分别是AB、AC的中点,且∠A+∠B=136°,则∠ANM=
如图,在△ABC中,M、N分别是AB、AC的中点,且∠A+∠B=136°,则∠ANM=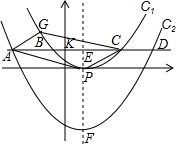 已知顶点为P的抛物线C1的解析式是y=a(x-3)2(a≠0),且经过点(0,1).
已知顶点为P的抛物线C1的解析式是y=a(x-3)2(a≠0),且经过点(0,1).