题目内容
11.如图,小明使一长为8厘米,宽为6厘米的长方形木板在桌面上作无滑动的滚动(顺时针方向),木板上的点A位置变化为A→A1→A2,其中第二次翻滚时被桌面上一小木块挡住,使木块与桌面成30°角,则点A翻滚到A2位置时共走过的路径长为( )
| A. | 20厘米 | B. | 8π厘米 | C. | 7π厘米 | D. | 5π厘米 |
分析 将点A翻滚到A2位置分成两部分:第一部分是以B为旋转中心,BA长10cm为半径旋转90°,第二部分是以C为旋转中心,6cm为半径旋转60°,根据弧长的公式计算即可.
解答 解:第一次是以B为旋转中心,BA长10cm为半径旋转90°,
此次点A走过的路径是$\frac{1}{4}•2π×10=5π$.
第二次是以C为旋转中心,6cm为半径旋转60°,
此次走过的路径是$\frac{1}{6}•2π•6=2π$,
∴点A两次共走过的路径是7π.
故选C
点评 本题主要考查了弧长公式l=$\frac{nπr}{180}$,注意两段弧长的半径不同,圆心角不同.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
2.下列说法,正确的是( )
| A. | -52 与(-5)2相等 | |
| B. | 如果两个数的和为零,那么这两个数一定是一正一负 | |
| C. | -a2表示一个负数 | |
| D. | 两个有理数的差不一定小于被减数 |




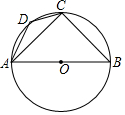 如图所示,AB是⊙O的直径,点C、D在⊙O上,若∠DAC=20°,∠B=50°,试求∠BCD的度数.
如图所示,AB是⊙O的直径,点C、D在⊙O上,若∠DAC=20°,∠B=50°,试求∠BCD的度数. 如图,在△ABC中,AB=5,BC=3,CA=4,AD平分∠BAC,点M,N分别为AD,AC上的动点,则CM+MN的最小值是2.4.
如图,在△ABC中,AB=5,BC=3,CA=4,AD平分∠BAC,点M,N分别为AD,AC上的动点,则CM+MN的最小值是2.4.
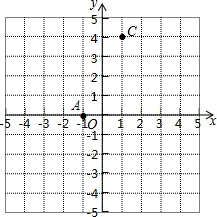 如图,A(-1,0),C(1,4),点B在x轴上,且AB=4.
如图,A(-1,0),C(1,4),点B在x轴上,且AB=4.