题目内容
4.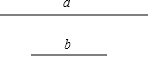 (1)用直尺和圆规作一个等腰三角形,使得底边长为线段a,底边上的高的长为线段b,要求保留作图痕迹.(不要求写出作法)
(1)用直尺和圆规作一个等腰三角形,使得底边长为线段a,底边上的高的长为线段b,要求保留作图痕迹.(不要求写出作法)(2)在(1)中,若a=6,b=4,求等腰三角形的腰长.
分析 (1)作一底边等于a,作底边的垂直平分线,从a上取高为b的线段,顺次连接三点,就是所画的三角形;
(2)根据等腰三角形的性质及勾股定理可得答案.
解答 解:(1)如图,等腰三角形ABC即为所求作三角形,其中AB=a,OC=b;
(2)由题意知AC=BC,CO⊥AB,且CO=4、AB=6,
∴AO=3,
则AC=$\sqrt{O{A}^{2}+O{C}^{2}}$=5,
即等腰三角形的腰长为5.
点评 本题主要考查等腰三角形的性质,用到的知识点为:等腰三角形底边上的中线和高互相重合.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
9.现给出以下几个命题:
(1)长度相等的两条弧是等弧;
(2)相等的弧所对的弦相等;
(3)平分于弦的直径垂直这条弦并且平分弦所对的两条弧;
(4)钝角三角形的外接圆圆心在三角形外面;
(5)矩形的四个顶点必在同一个圆上;
其中真命题的个数有( )
(1)长度相等的两条弧是等弧;
(2)相等的弧所对的弦相等;
(3)平分于弦的直径垂直这条弦并且平分弦所对的两条弧;
(4)钝角三角形的外接圆圆心在三角形外面;
(5)矩形的四个顶点必在同一个圆上;
其中真命题的个数有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
13.下列各式中结果为正数的是( )
| A. | -(-3) | B. | -|-3| | C. | -23 | D. | (-3)3 |
14.二次函数y=x2+4x-5的图象的对称轴为( )
| A. | x=-4 | B. | x=4 | C. | x=-2 | D. | x=2 |
 在平面直角坐标系中,已知点A(0,-2),B(0,4).
在平面直角坐标系中,已知点A(0,-2),B(0,4). (1)写出两个负数,使它们的差为-5,并写出具体算式.
(1)写出两个负数,使它们的差为-5,并写出具体算式.