题目内容
15.已知在Rt△ABC中,∠ACB=90°,AB=4,分别以AC,BC为边作等边三角形,面积分别记为S1,S2,则S1+S2的值等于4$\sqrt{3}$.分析 根据勾股定理有AC2+BC2=AB2=16,再根据等式性质可得$\frac{\sqrt{3}}{4}$AC2+$\frac{\sqrt{3}}{4}$BC2=$\frac{\sqrt{3}}{4}$AB2=4$\sqrt{3}$,再根据等边三角形的性质以及特殊三角函数值,易求而S1=$\frac{1}{2}$×sin60°AC•AC=$\frac{\sqrt{3}}{4}$AC2,同理可求S2=$\frac{\sqrt{3}}{4}$BC2,S3=$\frac{\sqrt{3}}{4}$AB2,从而可得S1+S2=S3=4$\sqrt{3}$.
解答 解:∵在Rt△ABC中,∠ACB=90°,AB=4,
∴AC2+BC2=AB2=16,
∴$\frac{\sqrt{3}}{4}$AC2+$\frac{\sqrt{3}}{4}$BC2=$\frac{\sqrt{3}}{4}$AB2=4$\sqrt{3}$,
又∵S1=$\frac{1}{2}$×sin60°AC•AC=$\frac{\sqrt{3}}{4}$AC2,S2=$\frac{\sqrt{3}}{4}$BC2,S3=$\frac{\sqrt{3}}{4}$AB2,
∴S1+S2=S3=4$\sqrt{3}$.
故答案为:4$\sqrt{3}$.
点评 本题考查了勾股定理、等边三角形的性质、特殊三角函数值.解题关键是根据等边三角形的性质求出每一个三角形的面积.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.先填表,通过观察后再回答问题
(1)被汗方数a的小数点位置移动和它的算术平方根$\sqrt{a}$的小数点位置移动有无规律?若有规律,请写出它的移动规律;
(2)已知:$\sqrt{a}$=1800,-$\sqrt{3.24}$=-1.8,你能求出a的值吗?
(3)试比较$\sqrt{a}$与a的大小.
| a | … | 0.000001 | 0.0001 | 0.01 | 1 | 100 | 10000 | 100000 | … |
| $\sqrt{a}$ | … | … |
(2)已知:$\sqrt{a}$=1800,-$\sqrt{3.24}$=-1.8,你能求出a的值吗?
(3)试比较$\sqrt{a}$与a的大小.
 如图,△ABC为等边三角形,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P,BF⊥AE于点F.若BP=4,则PF的长( )
如图,△ABC为等边三角形,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P,BF⊥AE于点F.若BP=4,则PF的长( ) 如图,在长14米、宽10米的矩形场地ABCD上,建有三条同样宽的小路,其中一条与AD平行,另两条与AB平行,其余的部分为草坪,已知草坪的总面积为117平方米,求小路的宽度.
如图,在长14米、宽10米的矩形场地ABCD上,建有三条同样宽的小路,其中一条与AD平行,另两条与AB平行,其余的部分为草坪,已知草坪的总面积为117平方米,求小路的宽度.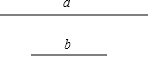 (1)用直尺和圆规作一个等腰三角形,使得底边长为线段a,底边上的高的长为线段b,要求保留作图痕迹.(不要求写出作法)
(1)用直尺和圆规作一个等腰三角形,使得底边长为线段a,底边上的高的长为线段b,要求保留作图痕迹.(不要求写出作法) 在Rt△ABC中,∠ACB=90°,CD是△ABC的高,E是AC的中点,ED、CB的延长线相交于点F,则图中相似三角形有( )
在Rt△ABC中,∠ACB=90°,CD是△ABC的高,E是AC的中点,ED、CB的延长线相交于点F,则图中相似三角形有( )