题目内容
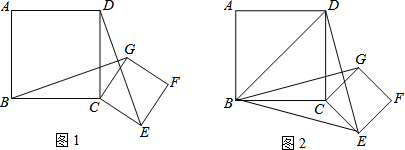
19.已知四边形ABCD和四边形CEFG都是正方形,且AB>CE.(1)如图1,连接BG、DE.求证:BG=DE;
(2)如图2,将正方形CEFG绕着点C旋转到某一位置时恰好使得CG∥BD,BG=BD,连接BE,求∠BED的度数.
分析 (1)先证∠BCG=∠DCE,再证明△BCG≌△DCE,即可得出结论;
(2)先证明∠BCG=∠BCE,再证明△BCG≌△BCE,得出BG=BE,证出△BDE为等边三角形,即可得出结果.
解答 (1)证明:∵四边形ABCD和CEFG为正方形,
∴BC=DC,CG=CE,∠BCD=∠GCE=90°,
∴∠BCD+∠DCG=∠GCE+∠DCG,
即:∠BCG=∠DCE,
在△BCG和△DCE中,$\left\{\begin{array}{l}{BC=DC}&{\;}\\{∠BCG=∠DCE}&{\;}\\{∠CG=CE}&{\;}\end{array}\right.$,
∴△BCG≌△DCE(SAS),
∴BG=DE;
(2)解:由(1)可知:BG=DE.
∵CG∥BD,
∴∠DCG=∠BDC=45°,
∴∠BCG=∠BCD+∠GCD=90°+45°=135°,
∵∠GCE=90°,
∴∠BCE=360°-∠BCG-∠GCE=360°-135°-90°=135°,
∴∠BCG=∠BCE,
在△BCG和△BCE中,$\left\{\begin{array}{l}{BC=BC}&{\;}\\{∠BCG=∠BCE}&{\;}\\{CG=CE}&{\;}\end{array}\right.$,
∴△BCG≌△BCE(SAS),
∴BG=BE,
∵BG=BD=DE,
∴BD=BE=DE,
∴△BDE为等边三角形,
∴∠BED=60°.
点评 本题考查了正方形的性质、等边三角形的判定与性质、全等三角形的判定与性质;证明三角形全等是解决问题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
10.若双曲线y=$\frac{k-1}{x}$的图象经过第二、四象限,则k的取值范围是( )
| A. | k>1 | B. | k<1 | C. | k=1 | D. | 不存在 |
4.一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三方面为选手打分,各项成绩均按百分制,进入决赛的两名选手的单项成绩如下表所示:
(1)如果认为这三方面的成绩同等重要,从他们的成绩看,谁能胜出?
(2)如果按演讲内容占50%,演讲能力占40%,演讲效果占10…%的比例计算甲、乙的平均成绩,那么谁将胜出?
| 选手 | 演讲内容 | 演讲能力 | 演讲效果 |
| 甲 | 85 | 95 | 95 |
| 乙 | 95 | 85 | 95 |
(2)如果按演讲内容占50%,演讲能力占40%,演讲效果占10…%的比例计算甲、乙的平均成绩,那么谁将胜出?
 线段的垂直平分线的性质1:
线段的垂直平分线的性质1: