题目内容
7.若x1、x2为关于x的一元二次方程x2-8x+k+3=0的两个实数根,且满足x1=3x2,试求出方程的两个实数根及k的值.分析 先由判别式的意义得出△=64-4×1×(k+3)≥0,解得,k≤13;再根据一元二次方程根与系数的关系,推出x1+x2=8,然后结合x1=3x2,即可推出x1和x2的值,最后根据k+3=x1•x2,即可求出k的值.
解答 解:∵关于x的一元二次方程x2-8x+k+3=0有两个实数根,
∴△=64-4×1×(k+3)≥0,
解得,k≤13;
由根与系数的关系,得
x1+x2=8 ①,x1•x2=k+3 ②,
又∵x1=3x2③,
联立①、③,解方程组得x1=6,x2=2,
∴k=x1x2-3=6×2-3=9.
答:方程两根为x1=6,x2=2;k=9.
点评 本题主要考查一元二次方程根与系数的关系:x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$,关键在于推出x1+x2=8,结合已知条件求出x1和x2的值.也考查了根的判别式.

练习册系列答案
相关题目
16.计算:(-2013)2013×(-2014)2014×(-2015)2015的结果可能是( )
| A. | 正数 | B. | 负数 | C. | 零 | D. | 不能确定 |
 如图,已知直线y=4-x与反比例函数y=$\frac{m}{x}$(m>0,x>0)的图象交于A、B两点,与x轴、y轴分别交于C、D两点.
如图,已知直线y=4-x与反比例函数y=$\frac{m}{x}$(m>0,x>0)的图象交于A、B两点,与x轴、y轴分别交于C、D两点.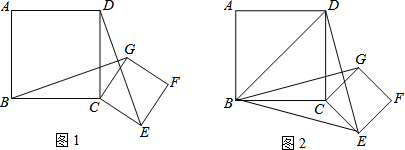
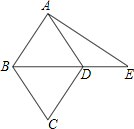 如图为菱形ABCD与Rt△ABE的重迭情形,其中D在BE上,∠BAE=90°.若AB=3,AE=4,则DE的长度为$\frac{7}{5}$.
如图为菱形ABCD与Rt△ABE的重迭情形,其中D在BE上,∠BAE=90°.若AB=3,AE=4,则DE的长度为$\frac{7}{5}$.