题目内容
14.已知a,b,c均为非负实数,且满足2a+3b-c=2,3a+b+2c=1,记S=3a+b-7c.求S的取值范围.分析 先解关于a、b的方程组$\left\{\begin{array}{l}{2a+3b-c=2}\\{3a+b+2c=1}\end{array}\right.$得$\left\{\begin{array}{l}{a=\frac{1}{7}-c}\\{b=\frac{4}{7}+c}\end{array}\right.$,再利用a,b,c均为非负实数得到0≤c≤$\frac{1}{7}$,接着用c表示S得到S=-9c+1,然后根据一次函数的性质确定S的范围.
解答 解:解方程组$\left\{\begin{array}{l}{2a+3b-c=2}\\{3a+b+2c=1}\end{array}\right.$得$\left\{\begin{array}{l}{a=\frac{1}{7}-c}\\{b=\frac{4}{7}+c}\end{array}\right.$,
∵a,b,c均为非负实数,
∴$\left\{\begin{array}{l}{\frac{1}{7}-c≥0}\\{\frac{4}{7}+c≥0}\\{c≥0}\end{array}\right.$,解得0≤c≤$\frac{1}{7}$,
∴S=3a+b-7c
=1-2c-7c
=-9c+1,
当c=0时,S=1,当c=$\frac{1}{7}$时,S=-$\frac{2}{7}$,
∴-$\frac{2}{7}$≤S≤1.
点评 本题考查了一次函数的性质:k>0,y随x的增大而增大,函数从左到右上升;k<0,y随x的增大而减小,函数从左到右下降.也考查了解二元一次方程组.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
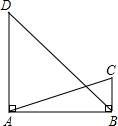 如图,已知∠ABC=∠BAD=90°,AC=13,BC=5,AD=16,求BD的长.
如图,已知∠ABC=∠BAD=90°,AC=13,BC=5,AD=16,求BD的长.
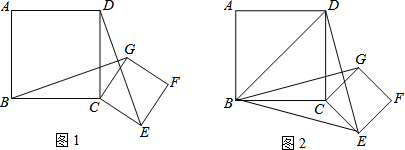
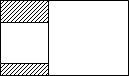 如图,矩形内有两个相邻的正方形,大正方形的面积为9,小正方形面积为3,那么阴影部分的面积为3$\sqrt{3}$-3.
如图,矩形内有两个相邻的正方形,大正方形的面积为9,小正方形面积为3,那么阴影部分的面积为3$\sqrt{3}$-3.