题目内容

如图，在△ABC中，点E、F分别为AB、AC的中点．若EF的长为2，则BC的长为（　　）
A、1B、2C、4D、8
考点：三角形中位线定理
专题：
分析：根据三角形的中位线平行于第三边并且等于第三边的一半可得BC=2EF．
解答：解：∵点E、F分别为AB、AC的中点，
∴EF是△ABC的中位线，
∴BC=2EF=2×2=4．
故选C．
点评：本题考查了三角形的中位线平行于第三边并且等于第三边的一半，熟记定理是解题的关键．
练习册系列答案
相关题目
若
102.02
≈10.10，
10.202
≈3.19，则±
1.0202
≈
 
；
若
33
≈1.442，
330
≈3.107，
3300
≈6.694，则
30.3
≈
 
，
3x
≈31.07，则x=
 
．
若a•b≠1，且有5a2+2011a+9=0，9b2+2011b+5=0，则
a
b
=
 
．
定义：我们把关于x的一元二次方程ax2+bx+c=0与cx2+bx+a=0（a≠c，ac≠0）称为一元二次方程的一对“友好方程”．如果一元二次方程的一对“友好方程”有公共解，则这个公共解是
 
．
如图，在Rt△ABC中，∠ABC是直角，AB=3，BC=4，P是BC边上的动点．设BP=x，若能在AC边上找到一点Q，使∠BQP=90°，则x的取值范围是（　　）
A、2.4≤x≤4
B、3≤x≤4
C、2.5≤x≤4
D、3＜x≤4
下列式子一定成立的是（　　）
A、3x2-x2=3
B、3a2+2a3=5a5
C、3+x=3x
D、-6ab+6ab=0
已知多边形的内角和是外角和的4倍，则这个多边形的边数为（　　）
A、6B、8C、10D、12
如图，在正方形ABCD中，边长为2的等边三角形AEF的顶点E、F分别在BC和CD上，下列结论：
①CE=CF；②∠AEB=75°；③BE+DF=EF；④BD=
3
+1．
其中正确的结论的个数为（　　）
A、1个B、2个C、3个D、4个
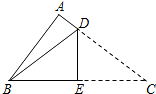在△ABC中，∠A=90°，AB=6，AC=8，若按如图那样折叠，使点C与点B 重合，折痕与AC、BC分别交于点D、E，则折痕DE的长为（　　）
A、
15
4
B、
20
3
C、4
D、5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网