Question

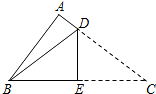在△ABC中，∠A=90°，AB=6，AC=8，若按如图那样折叠，使点C与点B 重合，折痕与AC、BC分别交于点D、E，则折痕DE的长为（　　）

• A、

  15

  4

• B、

  20

  3

• C、4
• D、5

Answer 1

考点：翻折变换（折叠问题）

专题：

分析：利用勾股定理列式求出BC，再根据翻折的性质求出CE，然后利用∠C的正切列式计算即可得解．

解答：解：∵∠A=90°，AB=6，AC=8，
∴由勾股定理得，BC=

AB2+AC2

=

62+82

=10，
∵折叠后点C与点B重合，
∴DE⊥BC且CE=

1

2

BC=

1

2

×10=5，
∵tan∠C=

DE

CE

=

AB

AC

，
∴

DE

5

=

6

8

，
解得DE=

15

4

．
故选A．

点评：本题考查了翻折变换的性质，勾股定理，锐角三角函数的定义，熟记性质并根据∠C的正切列式等式是解题的关键．