题目内容
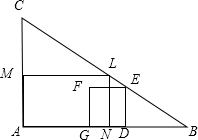 如图,在Rt△ABC中,∠A=90°,AB=8,AC=4,L、M、N分别是BC、AC、AB的中点,D是BA上一动点,过点D作DE∥AC交BC于E,设BD为x,以DE为一边在点B的异侧作正方形DEFG,正方形DEFG与四边形ANLM的公共部分面积为y.
如图,在Rt△ABC中,∠A=90°,AB=8,AC=4,L、M、N分别是BC、AC、AB的中点,D是BA上一动点,过点D作DE∥AC交BC于E,设BD为x,以DE为一边在点B的异侧作正方形DEFG,正方形DEFG与四边形ANLM的公共部分面积为y.(1)求y与x的函数关系式并写出自变量取值范围.
(2)当公共部分的面积为5,求正方形DEFG的面积.
考点:相似三角形的判定与性质
专题:常规题型
分析:(1)设BD=xcm,含x的代数式表示y(cm2),求出y和x的函数关系式,要分四种情况进行讨论:
①当G在D点或D点右侧时,
②当G在N点左侧,而D点在N点右侧或与N点重合时,
③当D在N点左侧,而G点在A点右侧或与A点重合时;
④当D在A左侧时,而G点在BA延长线上时,
(2)把将y=5代入(1)的式子中,看看求出的x哪个符合条件即可.
①当G在D点或D点右侧时,
②当G在N点左侧,而D点在N点右侧或与N点重合时,
③当D在N点左侧,而G点在A点右侧或与A点重合时;
④当D在A左侧时,而G点在BA延长线上时,
(2)把将y=5代入(1)的式子中,看看求出的x哪个符合条件即可.
解答:解:(1)设BD=xcm,含x的代数式表示y(cm2),求出y和x的函数关系式,
①当G在D点或D点右侧时,当正方形DEFG的边FG与矩形ANLM的边NL重合时,利用相似三角形的性质可得出x=
,即0<x≤
时,此时正方形与矩形没有重合,因此y=0;
②当G在N点左侧,而D点在N点右侧或与N点重合时,即
<x≤4,此时正方形与矩形重合的面积应该是以DN为长,DE为宽的矩形,DN=DG-NG=DG-(BN-BD)=x-(4-
x)=
x-4.而NM=PQ=
x,因此重合部分的面积应该是y=(
x-4)×
x=
x2-2x;
③当D在N点左侧,而G点在A点右侧或与A点重合时,即4<x≤
时,此时正方形重合部分的面积应该是以正方形边长为长,DE为宽的矩形的面积,PN=
x,DE=2,因此此时重合部分的面积是y=
x×2=x;
④当D在A左侧时,而G点在BA延长线上时,即
<x<8时,此时重合部分的面积应该是以LN长为宽,BD长为长的矩形的面积.AD=AB-BD=8-x,AM=LN=2,因此此时重合部分的面积应该是y=(8-x)×2=16-2x.
(2)当
<x≤4时,如果y=5,5=
x2-2x,解得x=
(舍去);
当4<x≤
时,如果y=5,x=5,符合题意,
当
<x<8时,如果y=5,5=16-2x,解得x=
,
因此当BD=5或
cm时,y=5cm2.
①当G在D点或D点右侧时,当正方形DEFG的边FG与矩形ANLM的边NL重合时,利用相似三角形的性质可得出x=
| 8 |
| 3 |
| 8 |
| 3 |
②当G在N点左侧,而D点在N点右侧或与N点重合时,即
| 8 |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
③当D在N点左侧,而G点在A点右侧或与A点重合时,即4<x≤
| 16 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
④当D在A左侧时,而G点在BA延长线上时,即
| 16 |
| 3 |
(2)当
| 8 |
| 3 |
| 3 |
| 4 |
4±2
| ||
| 3 |
当4<x≤
| 16 |
| 3 |
当
| 16 |
| 3 |
| 11 |
| 2 |
因此当BD=5或
| 11 |
| 2 |
点评:本题主要考查了直角三角形的性质,正方形的性质,中位线定理以及解直角三角形的应用等知识点,要注意x的值不同,正方形的位置不同时,函数解析式是不同的,要分类讨论,不要漏解.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
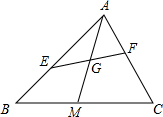 如图,在△ABC中,AM是中线,AB=8,AC=6,E、F分别在AB、AC上,且AE=2AF,EF交AM于点G,则
如图,在△ABC中,AM是中线,AB=8,AC=6,E、F分别在AB、AC上,且AE=2AF,EF交AM于点G,则 如图,在△ABC中,AD平分∠BAC,CE⊥AD,BF⊥AD,求证:
如图,在△ABC中,AD平分∠BAC,CE⊥AD,BF⊥AD,求证: 如图,△ABC中,DE∥BC,
如图,△ABC中,DE∥BC, 如图,Rt△ABC中,斜边AB上一点M,MN⊥AB交AC于N,若AM=3cm,AB:AC=5:4,求MN的长.
如图,Rt△ABC中,斜边AB上一点M,MN⊥AB交AC于N,若AM=3cm,AB:AC=5:4,求MN的长.