题目内容
如图，在△ABC中，AD平分∠BAC，CE⊥AD，BF⊥AD，求证：| BF |
| CE |
| AB |
| AC |
考点：相似三角形的判定与性质,角平分线的性质
专题：证明题
分析：根据题干中给出条件可以证明△ABF∽△ACD，即可证明
=
．
| BF |
| CE |
| AB |
| AC |
解答：证明：∵AD平分∠BAC，CE⊥AD，BF⊥AD，
∴∠BAF=∠CAD，∠AFB=∠AEC=90°
∴△ABF∽△ACD，
∴
=
．
∴∠BAF=∠CAD，∠AFB=∠AEC=90°
∴△ABF∽△ACD，
∴
| BF |
| CE |
| AB |
| AC |
点评：本题考查了相似三角形的判定，考查了相似三角形对应边比例相等的性质．
练习册系列答案
相关题目
如图，在直角坐标系中，以点A（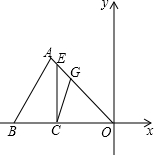
如图，点B、点C都在x轴上，其中点B（-30，0）、C（-20，0），A在第二象限中，△ABO中，∠ABO=45°，∠AOB=30°，过点C作x轴的垂线，与AO交于点E．
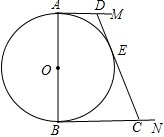如图，⊙O的直径AB=12cm，AM和BN是它的两条切线，DE与⊙O相切于点E，并与AM、BN分别交于D、C两点，设AD=x，BC=y，求y关于x的函数解析式，并画出它的图象．
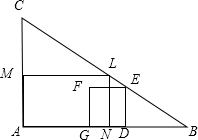如图，在Rt△ABC中，∠A=90°，AB=8，AC=4，L、M、N分别是BC、AC、AB的中点，D是BA上一动点，过点D作DE∥AC交BC于E，设BD为x，以DE为一边在点B的异侧作正方形DEFG，正方形DEFG与四边形ANLM的公共部分面积为y．
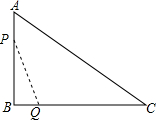如图在△ABC中，AB与BC垂直，AB=12，BC=24，动点P从点A开始沿AB方向向B点以2/s的速度运动，动点Q从B点开始沿BC向C点以4/s的速度运动，如果P、Q分别同时从A、B出发．
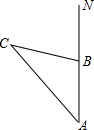如图，一艘船从港口A处出发，以20海里/时的速度向正北方向航行，该船经过4小时到达B处，港口A北偏西35°方向上有一小岛C，轮船在B处观测到小岛C在北偏西70°的方向上，求从B处到小岛C的距离．