题目内容
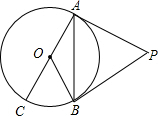 如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠BAC=20°,求∠P的度数.
如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠BAC=20°,求∠P的度数.考点:切线长定理
专题:
分析:根据切线长定理得等腰△PAB,运用三角形内角和定理求解即可.
解答:解:根据切线的性质得:∠PAC=90°,
所以∠PAB=90°-∠BAC=90°-20°=70°,
根据切线长定理得PA=PB,
所以∠PAB=∠PAB=70°,
所以∠P=180°-70°×2=40°.
所以∠PAB=90°-∠BAC=90°-20°=70°,
根据切线长定理得PA=PB,
所以∠PAB=∠PAB=70°,
所以∠P=180°-70°×2=40°.
点评:此题主要考查了切线长定理和切线的性质,得出PA=PB是解题关键.

练习册系列答案
相关题目
下列说法错误的是( )
| A、有两角和其中一角的对边对应相等的两个三角形全等 |
| B、全等三角形对应的角平分线相等 |
| C、斜边和一个锐角分别相等的两个直角三角形全等 |
| D、在△ABC和△A′B′C′中,若AB=BC=CA,A′B′=B′C′=C′A′,则△ABC≌△A′B′C′ |
在△ABC中,若三边BC、CA、AB满足BC:CA:AB=5:12:13,则cosB=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
某企业2011年向全国上缴利税400万元,2013年增加到484万元,则该企业两年上缴的利税平均每年增长的百分率为( )
| A、5% | B、10% |
| C、15% | D、20% |
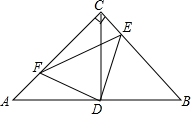 如图,在等腰Rt△ABC中,∠ACB=90°,D是AB边上的中点,点E、F分别在BC、AC边上运动,且保持AF=CE,连接DE,DF,EF,CD
如图,在等腰Rt△ABC中,∠ACB=90°,D是AB边上的中点,点E、F分别在BC、AC边上运动,且保持AF=CE,连接DE,DF,EF,CD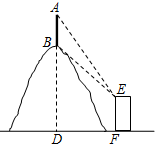 如图,在观测点E测得小山上铁塔顶A的仰角为60°,铁塔底部B的仰角为45°.已知塔高AB=20m,观测点E到地面的距离EF=35m,求小山BD的高.(结果保留根号)
如图,在观测点E测得小山上铁塔顶A的仰角为60°,铁塔底部B的仰角为45°.已知塔高AB=20m,观测点E到地面的距离EF=35m,求小山BD的高.(结果保留根号)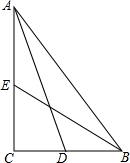 如图,在△ABC中,∠C=90°,AD,BE分别为边BC,AC上的中线,且AD=
如图,在△ABC中,∠C=90°,AD,BE分别为边BC,AC上的中线,且AD=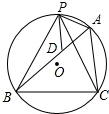 如图,△ABC内接于⊙O,AB=8,AC=6,D是AB边上的一点,P是优弧
如图,△ABC内接于⊙O,AB=8,AC=6,D是AB边上的一点,P是优弧