题目内容
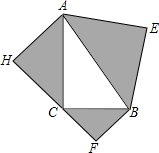如图，以Rt△ABC的三边为斜边分别向外作等腰直角三角形，若斜边AB=a，则图中阴影部分的面积为考点：勾股定理
专题：
分析：根据勾股定理可得AC2+BC2=AB2，然后判断出阴影部分的面积=2S△ABE，再利用等腰直角三角形的面积等于斜边平方的一半计算即可得解．
解答：解：∵△ABC是直角三角形，
∴AC2+BC2=AB2，
∵三个阴影部分三角形都是等腰直角三角形，
∴阴影部分的面积=2S△ABE=2×
•a•（
a）=
a2．
故答案为：
a2．
∴AC2+BC2=AB2，
∵三个阴影部分三角形都是等腰直角三角形，
∴阴影部分的面积=2S△ABE=2×
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为：
| 1 |
| 2 |
点评：本题考查了勾股定理，等腰直角三角形的性质，熟记定理与等腰直角三角形的面积的求法是解题的关键．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
如图，在?ABCD中，BC=2CD，点M、N分别在BC、CD边上，AM与BN交于点E．若∠C=∠AEN，BN=5
如图，⊙A、⊙B、⊙C、⊙D、⊙E相互外离，它们的半径都为1．顺次连接五个圆心得到五边形ABCDE，则图中五个阴影部分的面积之和是下列说法错误的是（ ）
| A、有两角和其中一角的对边对应相等的两个三角形全等 |
| B、全等三角形对应的角平分线相等 |
| C、斜边和一个锐角分别相等的两个直角三角形全等 |
| D、在△ABC和△A′B′C′中，若AB=BC=CA，A′B′=B′C′=C′A′，则△ABC≌△A′B′C′ |
如图，AB是⊙O的直径，
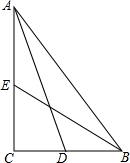如图，在△ABC中，∠C=90°，AD，BE分别为边BC，AC上的中线，且AD=