题目内容
某工艺品厂生产一款工艺品.已知这款工艺品的生产成本为每件60元.经市场调研发现:该款工艺品每天的销售量y(件)与售价x(元)之间存在着如下表所示的一次函数关系[利润=(售价-成本价)×销售量].
(1)求销售量y(件)与售价x(元)之间的函数表达式;
(2)当定价为80元时,工艺品厂每天获得的利润为多少?
| 售价x(元) | … | 70 | 90 | … |
| 销售量y(件) | … | 3 000 | 1 000 | … |
(2)当定价为80元时,工艺品厂每天获得的利润为多少?
考点:一次函数的应用
专题:
分析:(1)设y=kx+b(k≠0),然后利用待定系数法求一次函数解析式解答;
(2)根据定价求出销售量,再根据利润等于每一件的利润乘以销售量计算即可得解.
(2)根据定价求出销售量,再根据利润等于每一件的利润乘以销售量计算即可得解.
解答:解:(1)设y=kx+b(k≠0),
∵x=70时,y=3000,x=90时,y=1000,
∴
,
解得
,
所以y=-100x+10000;
(2)定价为80元时,y=-100×80+10000=2000,
每天获得的利润=(80-60)×2000=40000元.
∵x=70时,y=3000,x=90时,y=1000,
∴
|
解得
|
所以y=-100x+10000;
(2)定价为80元时,y=-100×80+10000=2000,
每天获得的利润=(80-60)×2000=40000元.
点评:本题考查了一次函数的应用,主要利用了待定系数法求一次函数解析式,已知自变量求函数值,待定系数法求函数解析式需熟练掌握.

练习册系列答案
相关题目
已知ax|a|-1+8=2(x-2)是关于x的一元一次方程,则( )
| A、a≠2 | B、a=±1或-2 |
| C、a=±1 | D、a=-2 |
若直线y=-3x+m与两坐标轴所围成的三角形的面积是6,则m的值为( )
| A、6 | B、-6 | C、±6 | D、±3 |
在△ABC中,∠C-30°=∠A+∠B,则△ABC是( )
| A、锐角三角形 |
| B、钝角三角形 |
| C、直角三角形 |
| D、有一个角30°的等腰三角形 |
 如图,在直角坐标系中,点P为菱形OACB的对角线AB、OC的交点,其中点B、P在双曲线y=
如图,在直角坐标系中,点P为菱形OACB的对角线AB、OC的交点,其中点B、P在双曲线y=| k |
| x |
A、(-1,
| ||||
B、(-2,
| ||||
C、(-
| ||||
D、(-3,
|
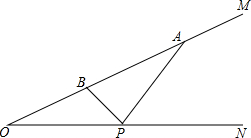 如图,已知∠MON=30°,在OM上有两点A、B分别到ON的距离为2cm和1cm,若在ON上找一点P使|PA-PB|的值最大,求P点到O点的距离.
如图,已知∠MON=30°,在OM上有两点A、B分别到ON的距离为2cm和1cm,若在ON上找一点P使|PA-PB|的值最大,求P点到O点的距离.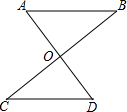 已知:如图,AD与BC相交于点O,OA=OD,OB=OC.求证:
已知:如图,AD与BC相交于点O,OA=OD,OB=OC.求证: