题目内容
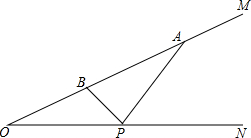如图，已知∠MON=30°，在OM上有两点A、B分别到ON的距离为2cm和1cm，若在ON上找一点P使|PA-PB|的值最大，求P点到O点的距离．考点：轴对称-最短路线问题
专题：
分析：根据三角形的三边关系，两边的差小于第三边，可以判定当P点在OM和ON的交点处|PA-PB|的值最大，从而求得P点到O点的距离．
解答：解：因为A、B在OM上，要使|PA-PB|的值最大，P应在OM上，
如果P不在OM上，则P、A、B构成三角形，根据三角形的三边关系，|PA-PB|＜AB，
所以，P是OM和ON的交点，即O点，
所以P到O的距离为0．
如果P不在OM上，则P、A、B构成三角形，根据三角形的三边关系，|PA-PB|＜AB，
所以，P是OM和ON的交点，即O点，
所以P到O的距离为0．
点评：本题考查了三角形的三边关系，两边的和大于第三边，两边的差小于第三边．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
从实数0.4，17，0，5，π2，3.1415926中选出两个无理数是（ ）
| A、17，5 |
| B、π2，17 |
| C、3.1415926，π2 |
| D、π2，5 |
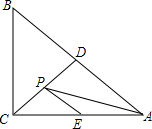如图，等腰直角△ABC中，∠ACB=90°，AB=2