题目内容
18. 如图,边长为$\sqrt{2}$的正方形ABCD的顶点A、B在一个半径为$\sqrt{2}$的圆上,顶点C、D在圆内,将正方形ABCD沿圆的内壁逆时针方向作无滑动的滚动.当点C第一次落在圆上时,点C运动的路径长为$({\frac{1}{3}+\frac{{\sqrt{2}}}{6}})π$.
如图,边长为$\sqrt{2}$的正方形ABCD的顶点A、B在一个半径为$\sqrt{2}$的圆上,顶点C、D在圆内,将正方形ABCD沿圆的内壁逆时针方向作无滑动的滚动.当点C第一次落在圆上时,点C运动的路径长为$({\frac{1}{3}+\frac{{\sqrt{2}}}{6}})π$.
分析 设圆心为O,连接AO,BO,AC,AE,易证三角形AOB是等边三角形,确定∠GFE=∠EAC=30°,再利用弧长公式计算即可.
解答 解:如图所示: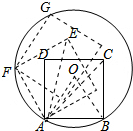
设圆心为O,连接AO,BO,AC,AE,
∵AB=$\sqrt{2}$,AO=BO=$\sqrt{2}$,
∴AB=AO=BO,
∴△AOB是等边三角形,
∴∠AOB=∠OAB=60°
同理:△FAO是等边三角形,∠FAB=2∠OAB=120°,
∴∠EAC=120°-90°=30,∠GFE=∠FAD=120°-90°=30°,
∵AD=AB=$\sqrt{2}$,
∴AC=$\sqrt{(\sqrt{2})^{2}+(\sqrt{2})^{2}}$=2,
当点C第一次落在圆上时,点C运动的路径长为$\frac{30π×2}{180}$+$\frac{30π×\sqrt{2}}{180}$=$({\frac{1}{3}+\frac{{\sqrt{2}}}{6}})π$;
故答案为:$({\frac{1}{3}+\frac{{\sqrt{2}}}{6}})π$.
点评 本题考查了正方形的性质、旋转的性质、等边三角形的判定和性质、勾股定理的运用以及弧长公式的运用,题目的综合性较强,解题的关键是正确的求出旋转角的度数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.用圆心角120°,半径为3的扇形纸片围成一圆锥的侧面,则这圆锥的底圆半径是( )
| A. | 1 | B. | 1.5 | C. | 2 | D. | 3 |
10.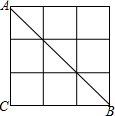 在正方形网格中,△ABC如图放置,点A,B,C都在格点上,则sin∠BAC的值为( )
在正方形网格中,△ABC如图放置,点A,B,C都在格点上,则sin∠BAC的值为( )
 在正方形网格中,△ABC如图放置,点A,B,C都在格点上,则sin∠BAC的值为( )
在正方形网格中,△ABC如图放置,点A,B,C都在格点上,则sin∠BAC的值为( )| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
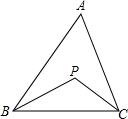 如图,已知:点P是△ABC内一点.
如图,已知:点P是△ABC内一点.