题目内容
10.阅读材料:如果一个花坛的长,宽分别是m、n,且m、n满足m2-2mn+2n2-4n+4=0,求花坛的面积.解:∵m2-2mn+2n2-4n+4=0,∴(m2-2mn+n2)+(n2-4n+4)=0
∴(m-n)2+(n-2)2=0,∴(m-n)2=0,(n-2)2=0,∴m=n,n=2.
∴mn=4
根据你的观察和思考,探究下面的问题:
(1)若x2-2xy+5y2+4y+1=0,求xy的值;
(2)若5x2+y2+z2+4xy-2xz=0,求代数式x-y-3z的值;
(3)若△ABC的三边长a、b、c都是正整数,且满足a2+b2-10a-12b+61=0,求△ABC的周长的最大值.
分析 (1)利用完全平方公式分组分解,进一步利用非负数的性质求得x、y的数值,进一步代入求得答案即可;
(2)利用完全平方公式分组分解,进一步利用非负数的性质求得x、y、z的关系,进一步代入求得答案即可;
(3)利用完全平方公式分组分解,进一步利用非负数的性质求得a、b的数值,进一步利用三角形的三边关系求得c,再求得周长即可.
解答 解:(1)∵x2-2xy+5y2+4y+1=0,
∴(x-y)2+(2y+1)2=0,
∴x-y=0,2y+1=0
∴x=y=-$\frac{1}{2}$,
∴xy=$\frac{1}{4}$.
(2)∵5x2+y2+z2+4xy-2xz=0,
∴(2x+y)2+(x-z)2=0,
∴2x+y=0,x-z=0
∴-y=2x,z=x,
∴x-y-3z=x+2x-3x=0.
(3)∵a2+b2-10a-12b+61=0,
∴(a-5)2+(b-6)2=0,
∴a-5=0,b-6=0
∴a=5,b=6.
∴1<c<11,
∵c为整数,
∴c的最大值为10,
∴△ABC的周长的最大值为21.
点评 此题考查配方法的运用,非负数的性质,掌握完全平方公式是解决问题的关键.

练习册系列答案
相关题目
2.国家出台全面二孩政策,自2016年1月1日起家庭生育无需审批.如果一个家庭已有一个孩子,再生一个孩子,那么两个都是女孩的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | 无法确定 |
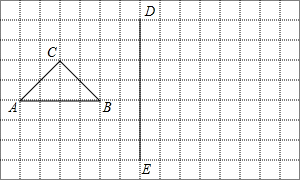 如图,在所给网格图(每小格均为边长为1的正方形),
如图,在所给网格图(每小格均为边长为1的正方形), 已知a,b两数在数轴上的表示如图所示,则-a>b.(填“>”、“=”或“<”)
已知a,b两数在数轴上的表示如图所示,则-a>b.(填“>”、“=”或“<”) 如图,边长为$\sqrt{2}$的正方形ABCD的顶点A、B在一个半径为$\sqrt{2}$的圆上,顶点C、D在圆内,将正方形ABCD沿圆的内壁逆时针方向作无滑动的滚动.当点C第一次落在圆上时,点C运动的路径长为$({\frac{1}{3}+\frac{{\sqrt{2}}}{6}})π$.
如图,边长为$\sqrt{2}$的正方形ABCD的顶点A、B在一个半径为$\sqrt{2}$的圆上,顶点C、D在圆内,将正方形ABCD沿圆的内壁逆时针方向作无滑动的滚动.当点C第一次落在圆上时,点C运动的路径长为$({\frac{1}{3}+\frac{{\sqrt{2}}}{6}})π$.