题目内容
10.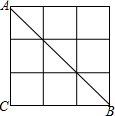 在正方形网格中,△ABC如图放置,点A,B,C都在格点上,则sin∠BAC的值为( )
在正方形网格中,△ABC如图放置,点A,B,C都在格点上,则sin∠BAC的值为( )| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
分析 在直角△ABC中,首先利用勾股定理求得AB的长,然后根据正弦的定义求解.
解答 解:AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}+{3}^{3}}$=3$\sqrt{2}$,
则sin∠BAC=$\frac{BC}{AB}$=$\frac{3}{3\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
故选C.
点评 本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案
相关题目
2.国家出台全面二孩政策,自2016年1月1日起家庭生育无需审批.如果一个家庭已有一个孩子,再生一个孩子,那么两个都是女孩的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | 无法确定 |
5.下列式子中正确的是( )
| A. | -3-2=-1 | B. | 3a+2b=5ab | C. | -|-7|=7 | D. | 5xy-5yx=0 |
15.在下列各数中,无理数是( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\sqrt{2}$ | D. | 7 |
 如图,把一块长方形纸片ABCD沿EG折叠,若∠FEG=35°,则∠AEF的补角为70度.
如图,把一块长方形纸片ABCD沿EG折叠,若∠FEG=35°,则∠AEF的补角为70度. 如图,边长为$\sqrt{2}$的正方形ABCD的顶点A、B在一个半径为$\sqrt{2}$的圆上,顶点C、D在圆内,将正方形ABCD沿圆的内壁逆时针方向作无滑动的滚动.当点C第一次落在圆上时,点C运动的路径长为$({\frac{1}{3}+\frac{{\sqrt{2}}}{6}})π$.
如图,边长为$\sqrt{2}$的正方形ABCD的顶点A、B在一个半径为$\sqrt{2}$的圆上,顶点C、D在圆内,将正方形ABCD沿圆的内壁逆时针方向作无滑动的滚动.当点C第一次落在圆上时,点C运动的路径长为$({\frac{1}{3}+\frac{{\sqrt{2}}}{6}})π$. 如图,已知AD、BC相交于点O,AB∥CD∥EF,如果CE=2,EB=4,FD=1.5,那么AD=4.5.
如图,已知AD、BC相交于点O,AB∥CD∥EF,如果CE=2,EB=4,FD=1.5,那么AD=4.5.