题目内容
16.(1)阅读下面材料:点A,B在数轴上分别表示实数a,b,A,B两点之间的距离表示为|AB|.
当A,B两点中有一点在原点时,不妨设点A在原点,如图(1),|AB|=|OB|=|b|=|a-b|;
当A,B两点都不在原点时,
①如图(2),点A,B都在原点的右边,|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|;
②如图(3),点A,B都在原点的左边,|AB|=|OB|-|OA|=|b|-|a|=-b-(-a)=|a-b|;
③如图(4),点A,B在原点的两边,|AB|=|OA|+|OB|=|a|+|b|=a+(-b)=|a-b|;
综上,数轴上A,B两点之间的距离|AB|=|a-b|.
(2)回答下列问题:
①数轴上表示2和5的两点之间的距离是3,数轴上表示-2和-5的两点之间的距离是3,数轴上表示1和-3的两点之间的距离是4;
②数轴上表示x和-1的两点A和B之间的距离是|x+1|,如果|AB|=2,那么x为1或-3;
③当代数式|x+1|+|x-2|取最小值时,相应的x的取值范围是-1≤x≤2.
④当x=3或-2 时,|x+1|+|x-2|=5.
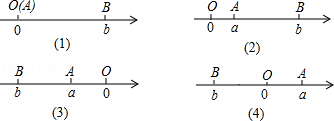
分析 ①根据数轴上A,B两点之间的距离|AB|=|a-b|回答即可;
②根据数轴上A,B两点之间的距离|AB|=|a-b|回答即可;
③|x+1|+|x-3|的最小值,意思是x到-1的距离与到3的距离之和最小,那么x应在-1和3之间的线段上.
④分三种情况讨论即可求得.
解答 解:①|2-5|=3,|-2-(-5)|=3,|1-(-3)|=4;
②|x-(-1)|=|x+1|,
如果AB=2,则x+1=±2,
解得x=1或-3;
③若|x+1|+|x-2|取最小值,那么表示x的点在-1和2之间的线段上,
所以-1≤x≤2.
④若x+1>0,x-2>0,则(x+1)+(x-2)=5,解得x=3,
若x+1<0,x-2<0,则-(x+1)-(x-2)=5,解得x=-2,
若x+1和x-2异号,则等式不成立,
所以当x=3或-2时,|x+1|+|x-2|=5.
故答案为:3,3,4;|x+1|,1或-3;-1≤x≤2;3或-2.
点评 本题主要考查了数轴和绝对值,掌握数轴上两点间的距离=两个数之差的绝对值.

练习册系列答案
相关题目
6.A,B是平面内的两个定点,在平面内找一点C,使△ABC构成等腰直角三角形,这样的C点可找( )
| A. | 2个 | B. | 4个 | C. | 6个 | D. | 8个 |
7.把分式$\frac{2ab}{a+b}$中a,b都扩大2倍,则分式的值( )
| A. | 扩大为原来的2倍 | B. | 扩大为原来的4倍 | C. | 缩小为原来的2倍 | D. | 不变 |
1.以边长为1的正方形ABCD的顶点A为圆心,以$\sqrt{2}$为半径作⊙A,则点C关于⊙A的位置关系是( )
| A. | 点C 在⊙A内 | B. | 点C在⊙A上 | C. | 点C在⊙A外 | D. | 不能确定 |
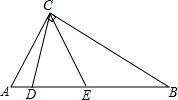 如图,在Rt△ABC中,AC=6,BC=8,D,E为斜边AB上的两个点,且BD=BC,AE=AC,则△DCE的外接圆的半径是2$\sqrt{2}$.
如图,在Rt△ABC中,AC=6,BC=8,D,E为斜边AB上的两个点,且BD=BC,AE=AC,则△DCE的外接圆的半径是2$\sqrt{2}$.