题目内容
实数k为何值时,方程x2+(2k-1)x+1+k2=0的两实数根的平方和最小,并求出这两个实数根.
考点:根与系数的关系,根的判别式
专题:
分析:利用一元二次方程根与系数的关系表示出两实根的平方和,得到一个关于k的二次函数,求出取得最小值时k的值,再利用根的判别式进行验证.
解答:解:设方程的两根分别为x1和x2,由一元二次方程根与系数的关系可得:x1+x2=-(2k-1),x1x2=1+k2,
令y=
,则y=(x1+x2)2-2x1x2=(2k-1)2-2(1+k2)=2k2-4k-1=2(k-1)2-3,
其为开口向上的二次函数,当k=1时,有最小值,
但当k=1时,一元二次方程的判别式为△=-7<0,
所以没有满足△≥0的k的值,
所以该题目无解.
令y=
| x | 2 1 |
| +x | 2 2 |
其为开口向上的二次函数,当k=1时,有最小值,
但当k=1时,一元二次方程的判别式为△=-7<0,
所以没有满足△≥0的k的值,
所以该题目无解.
点评:本题主要考查地一元二次方程根与系数的关系,解题时容易忽略还需要满足一元二次方程有实数根.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
若一个多边形的对角线的条数比它的顶点数多3,则这个多边形的边数为( )
| A、7 | B、6 | C、5 | D、4 |
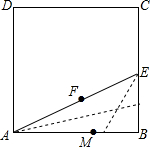 如图,用纸折出黄金分割点:裁一张边长为2的正方形纸片ABCD,先折出BC的中点E,再折出线段AE,然后通过折叠使EB落在线段EA上,折出点B的新位置F,因而EF=EB.类似的,在AB上折出点M使AM=AF.则M是AB的黄金分割点吗?若是请你证明,若不是请说明理由.
如图,用纸折出黄金分割点:裁一张边长为2的正方形纸片ABCD,先折出BC的中点E,再折出线段AE,然后通过折叠使EB落在线段EA上,折出点B的新位置F,因而EF=EB.类似的,在AB上折出点M使AM=AF.则M是AB的黄金分割点吗?若是请你证明,若不是请说明理由. 已知有理数a、b、c在数轴上对应的点如图,试化简:|b-a|-|a+c|-|b+c|.
已知有理数a、b、c在数轴上对应的点如图,试化简:|b-a|-|a+c|-|b+c|.