题目内容
下表中方程1、2、3是按照一定规律排列的方程,解方程3,并将它的解填在表中的空白处.
用你探究的规律,解下列方程x2+102x-36•18=0.
| 序号 | 方程 | 方程的解 |
| 1 | x2-2x-3=0 | x1=-1,x2=3 |
| 2 | x2-4x-12=0 | x1=-2,x2=6 |
| 3 | x2-6x-27=0 | x1= |
考点:一元二次方程的解
专题:规律型
分析:先利用因式分解法求出方程3的解为x1=-3,x2=9,再观察方程方程x2+102x-36•18=0,发现可利用因式分解法得到(x-6)(x+108)=0,进而求出方程的解.
解答:解:x2-6x-27=0,
(x+3)(x-9)=0,
所以,x1=-3,x2=9;
第n个方程为:x2-2nx-3n2=0,
方程的解是x1=-n,x2=3n;
∵x2+102x-36•18=0,
∴(x-6)(x+108)=0,
∴方程的解是x1=6,x2=-108.
故答案为-3,9.
(x+3)(x-9)=0,
所以,x1=-3,x2=9;
第n个方程为:x2-2nx-3n2=0,
方程的解是x1=-n,x2=3n;
∵x2+102x-36•18=0,
∴(x-6)(x+108)=0,
∴方程的解是x1=6,x2=-108.
故答案为-3,9.
点评:本题考查了一元二次方程的解,能够利用因式分解法正确分解是解题的关键.

练习册系列答案
相关题目
下列说法中错误的是( )
| A、有限小数都是有理数 |
| B、无限小数都是无理数 |
| C、正数包括正有理数和正无理数 |
| D、负数包括负有理数和负无理数 |
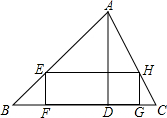 如图,一块三角形的铁皮,BC边为4厘米,BC边上的高AD为3厘米,要将它加工成一块矩形铁皮,使矩形的一边FG在BC上,其余两个顶点E,H分别在AB,AC上.设EF=x厘米,FG=y厘米.
如图,一块三角形的铁皮,BC边为4厘米,BC边上的高AD为3厘米,要将它加工成一块矩形铁皮,使矩形的一边FG在BC上,其余两个顶点E,H分别在AB,AC上.设EF=x厘米,FG=y厘米. 等腰Rt△ABC和等腰Rt△ADE中,AB=AE,AD=AE,∠BAC=∠DAE=90°
等腰Rt△ABC和等腰Rt△ADE中,AB=AE,AD=AE,∠BAC=∠DAE=90° 矩形的周长是16cm,设矩形的一边长为xcm,另一边长为ycm
矩形的周长是16cm,设矩形的一边长为xcm,另一边长为ycm 如图,在△ABC中,∠C=90°,AC=BC,BD平分∠ABC,DE⊥AB于点E,若△BCD与△ABC的面积之比是3:8,求△ADE与△ABC的面积之比.
如图,在△ABC中,∠C=90°,AC=BC,BD平分∠ABC,DE⊥AB于点E,若△BCD与△ABC的面积之比是3:8,求△ADE与△ABC的面积之比.