题目内容
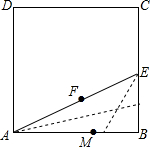 如图,用纸折出黄金分割点:裁一张边长为2的正方形纸片ABCD,先折出BC的中点E,再折出线段AE,然后通过折叠使EB落在线段EA上,折出点B的新位置F,因而EF=EB.类似的,在AB上折出点M使AM=AF.则M是AB的黄金分割点吗?若是请你证明,若不是请说明理由.
如图,用纸折出黄金分割点:裁一张边长为2的正方形纸片ABCD,先折出BC的中点E,再折出线段AE,然后通过折叠使EB落在线段EA上,折出点B的新位置F,因而EF=EB.类似的,在AB上折出点M使AM=AF.则M是AB的黄金分割点吗?若是请你证明,若不是请说明理由.考点:黄金分割,翻折变换(折叠问题)
专题:
分析:设正方形ABCD的边长为2,根据勾股定理求出AE的长,再根据E为BC的中点和翻折不变性,求出AM的长,二者相比即可得到黄金比.
解答:证明:∵正方形ABCD的边长为2,E为BC的中点,
∴BE=1
∴AE=
=
,
∵EF=BE=1,
∴AF=AE-EF=
-1,
∴AM=AF=
-1,
∴AM:AB=(
-1):2,
∴点M是线段AB的黄金分割点.
∴BE=1
∴AE=
| AB2+BE2 |
| 5 |
∵EF=BE=1,
∴AF=AE-EF=
| 5 |
∴AM=AF=
| 5 |
∴AM:AB=(
| 5 |
∴点M是线段AB的黄金分割点.
点评:本题考查了黄金分割的应用,知道黄金比并能求出黄金比是解题的关键,把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值(
)叫做黄金比.
| ||
| 2 |

练习册系列答案
相关题目
 如图,在△ABC中,∠C=90°,AC=BC,BD平分∠ABC,DE⊥AB于点E,若△BCD与△ABC的面积之比是3:8,求△ADE与△ABC的面积之比.
如图,在△ABC中,∠C=90°,AC=BC,BD平分∠ABC,DE⊥AB于点E,若△BCD与△ABC的面积之比是3:8,求△ADE与△ABC的面积之比.