题目内容
6. 如图,四边形ABCD中,AB=BC=1,CD=$\sqrt{3}$,DA=1,且∠B=90°.
如图,四边形ABCD中,AB=BC=1,CD=$\sqrt{3}$,DA=1,且∠B=90°.(1)求线段AC的长;
(2)判断△ACD的形状;
(3)求∠BAD的度数.
分析 (1)直接根据勾股定理求出AC的长即可;
(2)在△ACD中,由勾股定理的逆定理即可判断三角形的形状;
(3)根据等腰直角三角形的性质和角的和差关系即可求解.
解答 解:(1)∵∠B=90°,AB=BC=1,
∴AC2=AB2+BC2=1+1=2,∠BAC=45°,
∴AC=$\sqrt{2}$;
(2)∵△ACD中,AC=$\sqrt{2}$,CD=$\sqrt{3}$,AD=1,
∴AC2+AD2=2+1=3,CD2=3,
∴AC2+AD2=CD2,
∴△ACD是直角三角形,∠CAD=90°;
(3)∠BAD=∠BAC+∠CAD=45°+90°=135°.
点评 本题考查的是勾股定理的逆定理,勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
相关题目
14.一个两位数,十位数字是x,个位数字比十位数字的2倍少3,这个两位数是( )
| A. | x(2x-3) | B. | x(2x+3) | C. | 12x-3 | D. | 12x+3 |
18.已知正比例函数y=3x的图象经过点(-1,m),则m的值为( )
| A. | $\frac{1}{3}$ | B. | 3 | C. | -$\frac{1}{3}$ | D. | -3 |
15.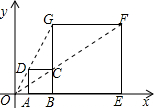 如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为$\frac{1}{3}$,点A、B、E在x轴上,若正方形BEFG的边长为6,则点C的坐标为( )
如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为$\frac{1}{3}$,点A、B、E在x轴上,若正方形BEFG的边长为6,则点C的坐标为( )
 如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为$\frac{1}{3}$,点A、B、E在x轴上,若正方形BEFG的边长为6,则点C的坐标为( )
如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为$\frac{1}{3}$,点A、B、E在x轴上,若正方形BEFG的边长为6,则点C的坐标为( )| A. | (2,2) | B. | (3,1) | C. | (3,2) | D. | (4,2) |
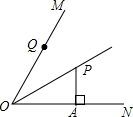 如图,OP平分∠MON,PA⊥ON,垂足为A,OA=8,PA=6,Q是射线OM上的一个动点,则线段PQ的最小值是( )
如图,OP平分∠MON,PA⊥ON,垂足为A,OA=8,PA=6,Q是射线OM上的一个动点,则线段PQ的最小值是( )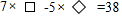 老师在课下给同学们留了如图所示的一个等式,让同学自己出题,并作出答案,请你回答处下列两个同学所提出问题的答案.
老师在课下给同学们留了如图所示的一个等式,让同学自己出题,并作出答案,请你回答处下列两个同学所提出问题的答案.