题目内容
17.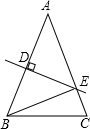 如图,在△ABC中,AB=AC=32cm,DE是AB的垂直平分线,分别交AB、AC于D、E两点.
如图,在△ABC中,AB=AC=32cm,DE是AB的垂直平分线,分别交AB、AC于D、E两点.(1)若∠C=70°,则∠A=40°,∠BEC=80°.
(2)若BC=21cm,则△BCE的周长是53cm.
分析 (1)利用等腰三角形的性质:等边对等角以及三角形的内角和定理以及外角的性质求解;
(2)根据线段的垂直平分线的性质可得AE=BE,据此即可求得.
解答 解:(1)∵AB=AC,
∴∠ABC=∠C=70°,
∴∠A=180°-∠ABC-∠C=180°-70°-70°=40°.
∵DE是AB的垂直平分线,
∴AE=BE,
∴∠ABE=∠A=40°,
∴∠BEC=∠A+∠ABE=40°+40°=80°.
故答案是:40°,80°;
(2)∵AE=BE,
∴△BCE的周长=BC+BE+CE=BC+AC=21+32=53(cm).
故答案是:53.
点评 本题考查的是线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
5.下列说法正确的是( )
| A. | 平分弦的直径垂直于弦 | |
| B. | 相等的圆心角所对的弧相等 | |
| C. | 半圆(或直径)所对的圆周角是直角 | |
| D. | 若直线和圆有公共点,则直线和圆相交 |
6.已知△ABC∽△DEF,相似比为3:1,且△DEF的周长为18,则△ABC的周长为( )
| A. | 3 | B. | 2 | C. | 6 | D. | 54 |