题目内容
20.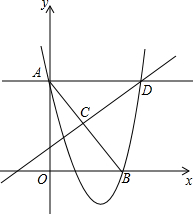 如图,点B是x轴上一动点,点A(0,2),过A作x轴的平行线交AB的中垂线CD于D,点C为垂足,抛物线y=ax2+bx+c经过A,B,D三点,当点B从(1,0)运动到(4,0)时,则a的变化范围是a≤-$\frac{1}{3}$或a≥$\frac{4}{3}$.
如图,点B是x轴上一动点,点A(0,2),过A作x轴的平行线交AB的中垂线CD于D,点C为垂足,抛物线y=ax2+bx+c经过A,B,D三点,当点B从(1,0)运动到(4,0)时,则a的变化范围是a≤-$\frac{1}{3}$或a≥$\frac{4}{3}$.
分析 设点B的坐标为(m,0),则点C($\frac{m}{2}$,1),根据线段垂直平分线的性质结合相似三角形的性质即可得出点D的坐标为($\frac{{m}^{2}+4}{2m}$,2),根据点A、B、D的坐标利用待定系数法即可求出a值,结合m的取值范围即可得出a的变化范围.
解答 解:设点B的坐标为(m,0),则点C($\frac{m}{2}$,1),
∵DC⊥AB,
∴∠ACD=∠BOA=90°.
∵∠BAO+∠CAD=∠BAO+∠OBA=90°,
∴∠CAD=∠OBA,
∴△CAD∽△OBA,
∴$\frac{AC}{BO}$=$\frac{AD}{AB}$,
∴AD=$\frac{AC•AB}{BO}$=$\frac{{m}^{2}+4}{2m}$,
∴点D的坐标为($\frac{{m}^{2}+4}{2m}$,2).
将A(0,2)、B(m,0)、D($\frac{{m}^{2}+4}{2m}$,2)代入y=ax2+bx+c,
$\left\{\begin{array}{l}{c=2}\\{a{m}^{2}+bm+c=0}\\{a(\frac{{m}^{2}+4}{2m})^{2}+b\frac{{m}^{2}+4}{2m}+c=2}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=-\frac{4}{{m}^{2}-4}}\\{b=\frac{4({m}^{2}+4)}{2m({m}^{2}-4)}}\\{c=2}\end{array}\right.$,
∴a=-$\frac{4}{{m}^{2}-4}$.
∵1≤m≤4,
∴a≤-$\frac{1}{3}$或a≥$\frac{4}{3}$.
故答案为:a≤-$\frac{1}{3}$或a≥$\frac{4}{3}$.
点评 本题考查了待定系数法求二次函数解析式、线段垂直平分线的性质以及相似三角形的判定与性质,根据线段垂直平分线的性质结合相似三角形的性质求出点D的坐标是解题的关键.

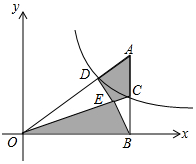 如图,点C在反比例函数y=$\frac{1}{x}$(x>0)的图象上,CB⊥x轴于点B,延长BC至A,使得AC=BC,连接AO交反比例函数的图象于点D,连接BD,OC交于点E,随着点C的横坐标的增大,图中阴影部分面积S1+S2的大小变化情况是( )
如图,点C在反比例函数y=$\frac{1}{x}$(x>0)的图象上,CB⊥x轴于点B,延长BC至A,使得AC=BC,连接AO交反比例函数的图象于点D,连接BD,OC交于点E,随着点C的横坐标的增大,图中阴影部分面积S1+S2的大小变化情况是( )| A. | 一直减小 | B. | 一直不变 | C. | 先减小后增大 | D. | 先增大后减小 |
| A. | (-x+y)(-x-y) | B. | (a-b)(b-a) | C. | (a-b)(a+b) | D. | (-x-1)(x-1) |
| A. | $\frac{1}{2}$是0.25的一个平方根 | B. | 正数a的两个平方根的和为0 | ||
| C. | $\frac{9}{16}$的平方根是$\frac{3}{4}$ | D. | 当x≠0时,-x2没有平方根 |
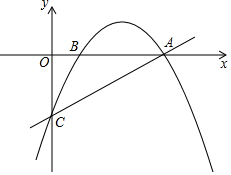 如图,抛物线经过点A(4,0)、B(1,0)、C(0,-2)三点.
如图,抛物线经过点A(4,0)、B(1,0)、C(0,-2)三点.