题目内容
8.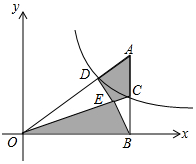 如图,点C在反比例函数y=$\frac{1}{x}$(x>0)的图象上,CB⊥x轴于点B,延长BC至A,使得AC=BC,连接AO交反比例函数的图象于点D,连接BD,OC交于点E,随着点C的横坐标的增大,图中阴影部分面积S1+S2的大小变化情况是( )
如图,点C在反比例函数y=$\frac{1}{x}$(x>0)的图象上,CB⊥x轴于点B,延长BC至A,使得AC=BC,连接AO交反比例函数的图象于点D,连接BD,OC交于点E,随着点C的横坐标的增大,图中阴影部分面积S1+S2的大小变化情况是( )| A. | 一直减小 | B. | 一直不变 | C. | 先减小后增大 | D. | 先增大后减小 |
分析 先过D作DF⊥OB于F,交OC于G,根据AB∥DF,且S△OFD=$\frac{1}{2}$S△AOB,得到$\frac{OD}{OA}$=$\frac{DF}{AB}$=$\frac{1}{\sqrt{2}}$,再根据DG∥BC,得出$\frac{DE}{BE}$=$\frac{DG}{BC}$=$\frac{1}{\sqrt{2}}$,进而得到S四边形ADEC=S△OAC-S△ODE=$\frac{\sqrt{2}}{2}$-$\frac{1}{2}$,S△OBE=$\frac{\sqrt{2}}{1+\sqrt{2}}$S△OBD=$\sqrt{2}$-1,最后根据S阴影=S四边形ADEC+S△OBE,即可得出S1+S2的大小不变.
解答  解:如图所示,过D作DF⊥OB于F,交OC于G,
解:如图所示,过D作DF⊥OB于F,交OC于G,
∵点C、D在反比例函数y=$\frac{1}{x}$(x>0)的图象上,CB⊥x轴于点B,
∴S△OBC=S△OFD=$\frac{1}{2}$,
∵AC=BC,
∴S△OBC=S△OAC=$\frac{1}{2}$,
∴S△OFD=$\frac{1}{2}$S△AOB,即S△AOB=1,
∵AB∥DF,
∴$\frac{OD}{OA}$=$\frac{DF}{AB}$=$\sqrt{\frac{1}{2}}$=$\frac{1}{\sqrt{2}}$,
∵DG∥BC,
∴$\frac{DE}{BE}$=$\frac{DG}{BC}$=$\frac{1}{\sqrt{2}}$,
∴S△ODE=$\frac{1}{1+\sqrt{2}}$S△OBD,S△OBD=$\frac{1}{\sqrt{2}}$S△AOB,
∴S△ODE=$\frac{1}{1+\sqrt{2}}$×$\frac{1}{\sqrt{2}}$S△AOB=(1-$\frac{\sqrt{2}}{2}$)×1=1-$\frac{\sqrt{2}}{2}$,
∴S四边形ADEC=S△OAC-S△ODE=$\frac{1}{2}$-(1-$\frac{\sqrt{2}}{2}$)=$\frac{\sqrt{2}}{2}$-$\frac{1}{2}$,
∵S△OBE=$\frac{\sqrt{2}}{1+\sqrt{2}}$S△OBD=$\frac{\sqrt{2}}{1+\sqrt{2}}$×$\frac{1}{\sqrt{2}}$S△AOB=($\sqrt{2}$-1)×1=$\sqrt{2}$-1,
∴S阴影=S四边形ADEC+S△OBE=$\frac{\sqrt{2}}{2}$-$\frac{1}{2}$+$\sqrt{2}$-1=$\frac{3}{2}\sqrt{2}$-$\frac{3}{2}$,
即S1+S2的大小不变,为$\frac{3}{2}\sqrt{2}$-$\frac{3}{2}$.
故选:B.
点评 本题主要考查了反比例函数系数k的几何意义,解题时注意:反比例函数y=$\frac{k}{x}$图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.在反比例函数的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是$\frac{1}{2}$|k|,且保持不变.

 春雨教育同步作文系列答案
春雨教育同步作文系列答案
| A. | 18 | B. | 19 | C. | 20 | D. | 21 |
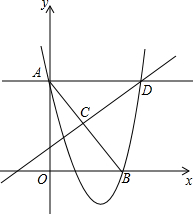 如图,点B是x轴上一动点,点A(0,2),过A作x轴的平行线交AB的中垂线CD于D,点C为垂足,抛物线y=ax2+bx+c经过A,B,D三点,当点B从(1,0)运动到(4,0)时,则a的变化范围是a≤-$\frac{1}{3}$或a≥$\frac{4}{3}$.
如图,点B是x轴上一动点,点A(0,2),过A作x轴的平行线交AB的中垂线CD于D,点C为垂足,抛物线y=ax2+bx+c经过A,B,D三点,当点B从(1,0)运动到(4,0)时,则a的变化范围是a≤-$\frac{1}{3}$或a≥$\frac{4}{3}$.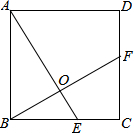 如图,正方形ABCD中,E、F分别是AB、BC边上的点,且AE=BF.
如图,正方形ABCD中,E、F分别是AB、BC边上的点,且AE=BF.