题目内容
9.在Rt△ABC中,∠C=90°,tanA=$\frac{2}{3}$,AC=6,则BC=( )| A. | 9 | B. | 4 | C. | 18 | D. | 12 |
分析 根据解直角三角形得出tanA=$\frac{2}{3}$=$\frac{BC}{AC}$,把AC=6代入求出即可.
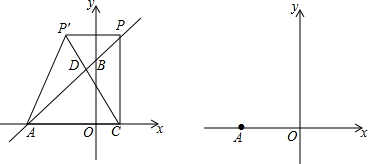
解答 解:如图:
∵在Rt△ACB中,∠C=90°,tanA=$\frac{2}{3}$=$\frac{BC}{AC}$,
∵AC=6,
∴BC=4.
故选:B.
点评 本题考查了锐角三角函数的定义的应用,注意:在Rt△ACB中,∠C=90°,则tanA=$\frac{∠A的对边}{∠A的邻边}$.

练习册系列答案
相关题目
20.△ABC的三边满足AC2-BC2=AB2,那么这个三角形的三个内角中( )
| A. | ∠A=90° | B. | ∠B=90° | C. | ∠C=90° | D. | 没有直角 |
1.读取表格中的信息,解决问题:
(1)计算:a1+b1+c1=3$\sqrt{2}$+3$\sqrt{3}$+3;
(2)满足$\frac{{{a_n}+{b_n}+{c_n}}}{{\sqrt{3}+\sqrt{2}}}≥81(\sqrt{3}-\sqrt{2}+1)$的n可以取得的最小正整数是4.
| n=1 | a1=$\sqrt{2}$+2$\sqrt{3}$ | b1=$\sqrt{3}$+2 | c1=1+2$\sqrt{2}$ |
| n=2 | a2=b1+2c1 | b2=c1+2a1 | c2=a1+2b1 |
| n=3 | a3=b2+2c2 | b3=c2+2a2 | c3=a2+2b2 |
| … | … | … | … |
(2)满足$\frac{{{a_n}+{b_n}+{c_n}}}{{\sqrt{3}+\sqrt{2}}}≥81(\sqrt{3}-\sqrt{2}+1)$的n可以取得的最小正整数是4.
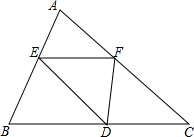 如图,△ABC中,E、F、D分别是AB、AC、BC上的点,且满足$\frac{AE}{EB}=\frac{AF}{FC}=\frac{2}{3}$,则S△ABC:S△EFD=25:6.
如图,△ABC中,E、F、D分别是AB、AC、BC上的点,且满足$\frac{AE}{EB}=\frac{AF}{FC}=\frac{2}{3}$,则S△ABC:S△EFD=25:6.