题目内容
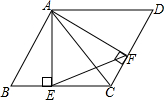 如图,在?ABCD,AE⊥BC,交BC于点E,AF⊥DC,交DC于点F,
如图,在?ABCD,AE⊥BC,交BC于点E,AF⊥DC,交DC于点F,(1)求证:△ABE∽△ADF;
(2)探讨:△AEF∽△ABC是否成立,并说明理由.
考点:相似三角形的判定
专题:
分析:(1)先根据平行四边形的性质求出∠B=∠D,再由AE⊥BC,AF⊥DC,故可得出结论;
(2)先根据平行四边形的性质得出∠BAC=∠DCA,再由AE⊥BC,AF⊥DC可知A、E、C、F四点共圆,故可得出∠DCA=∠AEF,∠AFE=∠ACE,故可得出结论.
(2)先根据平行四边形的性质得出∠BAC=∠DCA,再由AE⊥BC,AF⊥DC可知A、E、C、F四点共圆,故可得出∠DCA=∠AEF,∠AFE=∠ACE,故可得出结论.
解答:证明:(1)∵四边形ABCD是平行四边形,
∴∠B=∠D.
∵AE⊥BC,AF⊥DC,
∴∠AEB=∠AFD,
∴△ABE∽△ADF;
(2)当BC=AC时,△AEF∽△ABC是成立.
理由:∵四边形ABCD是平行四边形,
∴∠BAC=∠DCA.
∵AE⊥BC,AF⊥DC,
∴A、E、C、F四点共圆,
∴∠DCA=∠AEF,∠AFE=∠ACE,
∴∠AEF=∠BAC,∠AFE=∠ACB,
∴△AEF∽△BAC,
∵BC=AC,
∴∠B=∠BAC,
∴△AEF∽△ABC.
∴∠B=∠D.
∵AE⊥BC,AF⊥DC,
∴∠AEB=∠AFD,
∴△ABE∽△ADF;
(2)当BC=AC时,△AEF∽△ABC是成立.
理由:∵四边形ABCD是平行四边形,
∴∠BAC=∠DCA.
∵AE⊥BC,AF⊥DC,
∴A、E、C、F四点共圆,
∴∠DCA=∠AEF,∠AFE=∠ACE,
∴∠AEF=∠BAC,∠AFE=∠ACB,
∴△AEF∽△BAC,
∵BC=AC,
∴∠B=∠BAC,
∴△AEF∽△ABC.
点评:本题考查的是相似三角形的判定,熟知有两组角对应相等的两个三角形相似是解答此题的关键.

练习册系列答案
相关题目
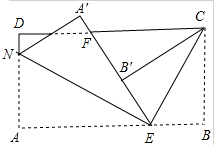 如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM,将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,求∠NEM的度数.
如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM,将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,求∠NEM的度数. 如图,点A、B、C是直线l上的三个点,图中共有射线条数为( )
如图,点A、B、C是直线l上的三个点,图中共有射线条数为( )| A、2条 | B、3条 | C、4条 | D、6条 |
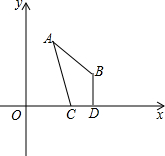 如图,平面直角坐标系中A(1,4),B(3,2),C、D为x轴上两动点,且CD=1,试求四边形ACDB周长最小时,C、D两点的坐标.
如图,平面直角坐标系中A(1,4),B(3,2),C、D为x轴上两动点,且CD=1,试求四边形ACDB周长最小时,C、D两点的坐标.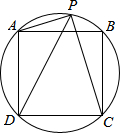 正方形ABCD的四点在☉O上,若P是弧AB上一点,请确定PA+PC与PD之间的数量关系,并证明你的结论.
正方形ABCD的四点在☉O上,若P是弧AB上一点,请确定PA+PC与PD之间的数量关系,并证明你的结论.