题目内容
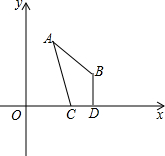 如图,平面直角坐标系中A(1,4),B(3,2),C、D为x轴上两动点,且CD=1,试求四边形ACDB周长最小时,C、D两点的坐标.
如图,平面直角坐标系中A(1,4),B(3,2),C、D为x轴上两动点,且CD=1,试求四边形ACDB周长最小时,C、D两点的坐标.考点:轴对称-最短路线问题,坐标与图形性质
专题:
分析:作点A关于x轴的对称点A′,则A′的坐标为(1,-4),把A′向右平移1个单位得到点B′(2,-4),连接BB′,与x轴交于点D,易得四边形A′B′DC为平行四边形,得到CA′=DB′=CA,则AC+BD=BB′,根据两点之间线段最短得到此时AC+BD最小,即四边形ABDC的周长最短.然后用待定系数法求出直线BB′的解析式y=6x-16,易得D点坐标为(
,0),则根据CD=1即可求得C的坐标为(
,0).
| 8 |
| 3 |
| 5 |
| 3 |
解答: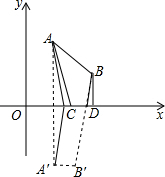 解:作点A关于x轴的对称点A′,则A′的坐标为(1,-4),把A′向右平移1个单位得到点B'(2,-4),连接BB′,与x轴交于点D,过A′作A′C∥B′D交x轴于C,如图,
解:作点A关于x轴的对称点A′,则A′的坐标为(1,-4),把A′向右平移1个单位得到点B'(2,-4),连接BB′,与x轴交于点D,过A′作A′C∥B′D交x轴于C,如图,
∴CA′=CA,
∵A′B′∥CD,
∴四边形A′B′DC为平行四边形,
∴CA′=DB′,
∴CA=DB′,
∴AC+BD=BB′,此时AC+BD最小,
而CD与AB的长一定,
∴此时四边形ABDC的周长最短.
设直线BB′的解析式为y=kx+b,
把B(3,2)、B'(2,-4)分别代入得
,
解得k=6,b=-16,
∴直线BB′的解析式为y=6x-16,
令y=0,则6x-16=0,
解得x=
,
∴D点坐标为(
,0),
∵CD=1,
∴C(
,0).
 解:作点A关于x轴的对称点A′,则A′的坐标为(1,-4),把A′向右平移1个单位得到点B'(2,-4),连接BB′,与x轴交于点D,过A′作A′C∥B′D交x轴于C,如图,
解:作点A关于x轴的对称点A′,则A′的坐标为(1,-4),把A′向右平移1个单位得到点B'(2,-4),连接BB′,与x轴交于点D,过A′作A′C∥B′D交x轴于C,如图,∴CA′=CA,
∵A′B′∥CD,
∴四边形A′B′DC为平行四边形,
∴CA′=DB′,
∴CA=DB′,
∴AC+BD=BB′,此时AC+BD最小,
而CD与AB的长一定,
∴此时四边形ABDC的周长最短.
设直线BB′的解析式为y=kx+b,
把B(3,2)、B'(2,-4)分别代入得
|
解得k=6,b=-16,
∴直线BB′的解析式为y=6x-16,
令y=0,则6x-16=0,
解得x=
| 8 |
| 3 |
∴D点坐标为(
| 8 |
| 3 |
∵CD=1,
∴C(
| 5 |
| 3 |
点评:本题考查了轴对称-最短路线问题:通过对称,把两条线段的和转化为一条线段,利用两点之间线段最短解决问题.也考查了坐标变换以及待定系数法求一次函数的解析式.

练习册系列答案
相关题目
 如图,已知∠APC、∠BPD都是直角,∠APD=110°,求∠BPC的度数.
如图,已知∠APC、∠BPD都是直角,∠APD=110°,求∠BPC的度数. 如图,在?ABCD,AE⊥BC,交BC于点E,AF⊥DC,交DC于点F,
如图,在?ABCD,AE⊥BC,交BC于点E,AF⊥DC,交DC于点F, 将一个三角尺和一把直尺如图放置,则∠α+∠β的度数是
将一个三角尺和一把直尺如图放置,则∠α+∠β的度数是