题目内容
解方程:|x-1|+
=x.
| x+1 |
考点:无理方程
专题:
分析:分类讨论:-1≤x<1,x≥1,可化简去掉绝对值,再根据平方运算,可得整式方程,解整式方程,可得答案.
解答:解:①当-1≤x<1时,则1-x+
=x,
化简,得
=2x-1,
平方,得x+1=4x2-4x+1.
解得:x1=0,x2=
(不符合题意的要舍去),
②当x>1时,则x-1+
=x,
化简,得
=1,
平方,得x+1=1,
解得:x=0(不符合题意的要舍去),
综上所述:x=0.
| x+1 |
化简,得
| x+1 |
平方,得x+1=4x2-4x+1.
解得:x1=0,x2=
| 5 |
| 4 |
②当x>1时,则x-1+
| x+1 |
化简,得
| x+1 |
平方,得x+1=1,
解得:x=0(不符合题意的要舍去),
综上所述:x=0.
点评:此题主要考查了无理方程的解法,正确转化方程形式是解题关键.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案
相关题目
 如图,已知∠APC、∠BPD都是直角,∠APD=110°,求∠BPC的度数.
如图,已知∠APC、∠BPD都是直角,∠APD=110°,求∠BPC的度数.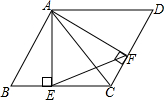 如图,在?ABCD,AE⊥BC,交BC于点E,AF⊥DC,交DC于点F,
如图,在?ABCD,AE⊥BC,交BC于点E,AF⊥DC,交DC于点F, 将一个三角尺和一把直尺如图放置,则∠α+∠β的度数是
将一个三角尺和一把直尺如图放置,则∠α+∠β的度数是 一个函数的图象是双曲线(如图),根据图象,求出这个函数的解析式和m的值.
一个函数的图象是双曲线(如图),根据图象,求出这个函数的解析式和m的值.