题目内容
已知在平面直角坐标系中,A(0,4),B(4,0),Q(0,2.5),点P在AB上,∠QPO=45°,求点P的坐标.
考点:相似三角形的判定与性质,坐标与图形性质
专题:
分析:作出图形,易证∠AQP=∠BPO,即可证明△AQP∽△BPO,可得
=
,即可求得PA•PB的值,再根据PA+PB=
AO,即可求得PA,PB的值,即可解题.
| AQ |
| BP |
| PA |
| BO |
| 2 |
解答:解:作出图形,
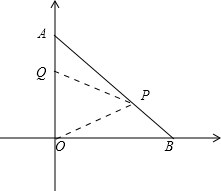
∵∠QPO=45°,
∴∠APQ+∠BPO=135°,
∵∠A=45°,
∴∠AQP+∠APQ=135°,
∴∠AQP=∠BPO,
∴△AQP∽△BPO,
∴
=
,代入AQ,BO得:PA•PB=6,
∵PA+PB=
AO=4
,
解得:PA=
,PB=3
,或PA=3
,PB=
,
∴点P坐标为(1,3)或(3,1).

∵∠QPO=45°,
∴∠APQ+∠BPO=135°,
∵∠A=45°,
∴∠AQP+∠APQ=135°,
∴∠AQP=∠BPO,
∴△AQP∽△BPO,
∴
| AQ |
| BP |
| PA |
| BO |
∵PA+PB=
| 2 |
| 2 |
解得:PA=
| 2 |
| 2 |
| 2 |
| 2 |
∴点P坐标为(1,3)或(3,1).
点评:本题考查了相似三角形的判定,考查了相似三角形对应边比例相等的性质,本题中求证是解题的关键.

练习册系列答案
相关题目
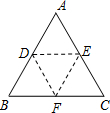 如图,折叠三角形纸片ABC,使点A落在BC边上的点F处,且折痕DE∥BC.若∠C=46°,则∠CFE=( )
如图,折叠三角形纸片ABC,使点A落在BC边上的点F处,且折痕DE∥BC.若∠C=46°,则∠CFE=( )| A、43° | B、44° |
| C、45° | D、46° |
 如图,在△ABC中,∠C=2∠B,D是BC边上一点,且AD⊥AB.
如图,在△ABC中,∠C=2∠B,D是BC边上一点,且AD⊥AB.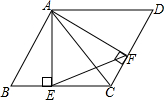 如图,在?ABCD,AE⊥BC,交BC于点E,AF⊥DC,交DC于点F,
如图,在?ABCD,AE⊥BC,交BC于点E,AF⊥DC,交DC于点F, 已知直线a∥b,填空:图(1)中∠1=
已知直线a∥b,填空:图(1)中∠1=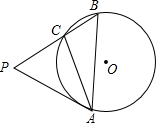 如图,在△ABC中,∠BAC=30°,∠ABC=45°,BC=1,⊙O是△ABC的外接圆,过点A作⊙O的切线,交BC的延长线于点P.
如图,在△ABC中,∠BAC=30°,∠ABC=45°,BC=1,⊙O是△ABC的外接圆,过点A作⊙O的切线,交BC的延长线于点P. 已知AD,AF分别是△ABC的高和角平分线,且∠B=30°,∠C=56°
已知AD,AF分别是△ABC的高和角平分线,且∠B=30°,∠C=56°