题目内容
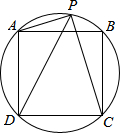 正方形ABCD的四点在☉O上,若P是弧AB上一点,请确定PA+PC与PD之间的数量关系,并证明你的结论.
正方形ABCD的四点在☉O上,若P是弧AB上一点,请确定PA+PC与PD之间的数量关系,并证明你的结论.考点:正多边形和圆,全等三角形的判定与性质,等腰直角三角形
专题:
分析:如图,首先证明∠APD=∠DPC=45°,借助余弦定理证明λ2-
PD•λ+PD2-γ2=0①μ2-
PD•μ+PD2-γ2=0②,得到λ、μ为方程x2-
PD•x+PD2-γ2=0的两个实数根,由根与系数的关系得到λ+μ=
PD,即可解决问题.
| 2 |
| 2 |
| 2 |
| 2 |
解答: 解:设PA=λ,PC=μ,正方形ABCD的边长为γ;
解:设PA=λ,PC=μ,正方形ABCD的边长为γ;
∵四边形ABCD是⊙O的内接正方形,
∴
=
=
⊙O的周长,
∴∠APD=∠DPC=45°;
由余弦定理得:
γ2=λ2+PD2-2λPD•cos45°,
∴λ2-
PD•λ+PD2-γ2=0①,
同理可求:
μ2-
PD•μ+PD2-γ2=0②,
由①、②知:
λ、μ为方程x2-
PD•x+PD2-γ2=0的两个实数根,
∴λ+μ=
PD.
即PA+PC=
PD.
 解:设PA=λ,PC=μ,正方形ABCD的边长为γ;
解:设PA=λ,PC=μ,正方形ABCD的边长为γ;∵四边形ABCD是⊙O的内接正方形,
∴
 |
| AD |
 |
| CD |
| 1 |
| 4 |
∴∠APD=∠DPC=45°;
由余弦定理得:
γ2=λ2+PD2-2λPD•cos45°,
∴λ2-
| 2 |
同理可求:
μ2-
| 2 |
由①、②知:
λ、μ为方程x2-
| 2 |
∴λ+μ=
| 2 |
即PA+PC=
| 2 |
点评:该题主要考查了圆内接正方形的性质及其应用问题;解题的关键是灵活运用有关定来分析、判断、推理或解答;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
相关题目
 如图,点A,B,C在⊙O上,若∠ABC=40°,则∠AOC的度数为
如图,点A,B,C在⊙O上,若∠ABC=40°,则∠AOC的度数为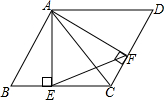 如图,在?ABCD,AE⊥BC,交BC于点E,AF⊥DC,交DC于点F,
如图,在?ABCD,AE⊥BC,交BC于点E,AF⊥DC,交DC于点F, 已知直线a∥b,填空:图(1)中∠1=
已知直线a∥b,填空:图(1)中∠1= 将一个三角尺和一把直尺如图放置,则∠α+∠β的度数是
将一个三角尺和一把直尺如图放置,则∠α+∠β的度数是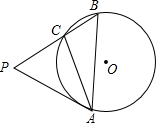 如图,在△ABC中,∠BAC=30°,∠ABC=45°,BC=1,⊙O是△ABC的外接圆,过点A作⊙O的切线,交BC的延长线于点P.
如图,在△ABC中,∠BAC=30°,∠ABC=45°,BC=1,⊙O是△ABC的外接圆,过点A作⊙O的切线,交BC的延长线于点P.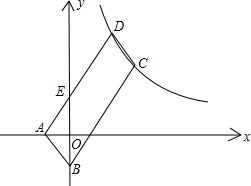 如图,?ABCD的顶点A、B的坐标分别是A(-1,0),B(0,-2),顶点C、D在双曲线y=
如图,?ABCD的顶点A、B的坐标分别是A(-1,0),B(0,-2),顶点C、D在双曲线y=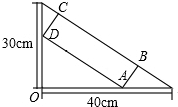 在一个直角三角形的内部作一个矩形ABCD,其顶点A和点D分别在两直角边上,BC在斜边上.
在一个直角三角形的内部作一个矩形ABCD,其顶点A和点D分别在两直角边上,BC在斜边上.