题目内容
20.解下列方程:(1)2x2+24x+54=0(用配方法计算);
(2)2x2+4x-3=0.
分析 (1)先把方程变形为x2+12x=-27,再利用配方法得到(x+6)2=9,然后利用直接开平方法解方程;
(2)先计算判别式的值,然后利用求根公式法解方程.
解答 解:(1)x2+12x+27=0,
x2+12x=-27,
x2+12x+36=-27+36,
(x+6)2=9,
x+6=±3,
x1=-3,x2=-9;
(2)△=42-4×2×(-3)=40,
x=$\frac{-4±\sqrt{40}}{2×2}$=$\frac{-2±\sqrt{10}}{2}$,
所以x1=$\frac{-1+\sqrt{10}}{2}$,x2=$\frac{-1-\sqrt{10}}{2}$.
点评 本题考查了解一元二次方程-公式法:用求根公式解一元二次方程的方法是公式法.也考查了配方法解一元二次方程.

练习册系列答案
相关题目
10. 在某次义务植树活动中,10名同学植树的棵树整理成条形统计图如图所示,他们植树的棵树的平均数为a,中位数为b,众数为c,则下列结论正确的是( )
在某次义务植树活动中,10名同学植树的棵树整理成条形统计图如图所示,他们植树的棵树的平均数为a,中位数为b,众数为c,则下列结论正确的是( )
 在某次义务植树活动中,10名同学植树的棵树整理成条形统计图如图所示,他们植树的棵树的平均数为a,中位数为b,众数为c,则下列结论正确的是( )
在某次义务植树活动中,10名同学植树的棵树整理成条形统计图如图所示,他们植树的棵树的平均数为a,中位数为b,众数为c,则下列结论正确的是( )| A. | a=b | B. | b>a | C. | b=c | D. | c>b |
15.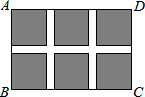 如图,某小区规划在一个长30m、宽20m的长方形土地ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分钟花草,要使每一块花草的面积都为78cm2,那么通道宽应设计成多少m?设通道宽为xm,则由题意列得方程为( )
如图,某小区规划在一个长30m、宽20m的长方形土地ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分钟花草,要使每一块花草的面积都为78cm2,那么通道宽应设计成多少m?设通道宽为xm,则由题意列得方程为( )
 如图,某小区规划在一个长30m、宽20m的长方形土地ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分钟花草,要使每一块花草的面积都为78cm2,那么通道宽应设计成多少m?设通道宽为xm,则由题意列得方程为( )
如图,某小区规划在一个长30m、宽20m的长方形土地ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分钟花草,要使每一块花草的面积都为78cm2,那么通道宽应设计成多少m?设通道宽为xm,则由题意列得方程为( )| A. | (30-x)(20-x)=78 | B. | (30-2x)(20-2x)=78 | C. | (30-2x)(20-x)=6×78 | D. | (30-2x)(20-2x)=6×78 |
5.下列命题正确的是( )
| A. | 对角线互相垂直的四边形是菱形 | |
| B. | 有三个角是直角的四边形是矩形 | |
| C. | 有两条边相等的四边形是平行四边形 | |
| D. | 四条边都相等的平行四边形是正方形 |
 如图,点O、A在数轴上表示的数分别是0,0.1,将线段OA分成100等份,其分点由左向右依次为M1,M2…M99,再将线段OM1分成100等份,其分点由左向右依次为N1,N2,…N99,则点N15所表示的数用科学记数法表示为1.5×10-4.
如图,点O、A在数轴上表示的数分别是0,0.1,将线段OA分成100等份,其分点由左向右依次为M1,M2…M99,再将线段OM1分成100等份,其分点由左向右依次为N1,N2,…N99,则点N15所表示的数用科学记数法表示为1.5×10-4.
 如图,已知△ABC和点O,画出△DEF,使△DEF和△ABC关于点O成中心对称.(画出图形并写出解答过程)
如图,已知△ABC和点O,画出△DEF,使△DEF和△ABC关于点O成中心对称.(画出图形并写出解答过程)