题目内容
20.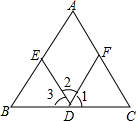 如图,(1)因为∠A=∠BED(已知),
如图,(1)因为∠A=∠BED(已知),所以AC∥ED同位角相等两直线平行
(2)因为∠2=∠DFC(已知),
所以AC∥ED内错角相等两直线平行
(3)因为∠A+∠AFD=180°(已知),
所以AB∥FD同旁内角互补两直线平行
(4)因为AB∥DF(已知),
所以∠2+∠AED=180°两直线平行同旁内角互补
(5)因为AC∥DE(已知),
所以∠C=∠3两直线平行同位角相等.
分析 (1)根据同位角相等两直线平行解答;
(2)根据内错角相等两直线平行解答;
(3)根据同旁内角互补两直线平行解答;
(4)根据两直线平行同旁内角互补解答;
(5)根据两直线平行同位角相等解答.
解答 解:(1)因为∠A=∠BE(已知),
所以AC∥ED(同位角相等两直线平行);
(2)因为∠2=∠DFC(已知),
所以AC∥ED (内错角相等两直线平行);
(3)因为∠A+∠AFD=180°(已知),
所以AB∥FD(同旁内角互补两直线平行);
(4)因为AB∥DF(已知),
所以∠2+∠AED=180°(两直线平行同旁内角互补);
(5)因为AC∥DE(已知),
所以∠C=∠3(两直线平行同位角相等).
故答案为:(1)∠BED,同位角相等,两直线平行;
(2)∠CFD,内错角相等,两直线平行;
(3)∠AFD,同旁内角互补,两直线平行;
(4)FD,两直线平行,同旁内角互补;
(5)ED,两直线平行,同位角相等.
点评 此题考查了平行线的判定与性质:内错角相等?两直线平行;同位角相等?两直线平行;同旁内角互补?两直线平行.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
11.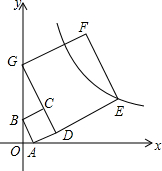 如图,已知点A(1,0),B(0,2),以AB为边在第一象限内作正方形ABCD,直线CD与y轴交于点G,再以DG为边在第一象限内作正方形DEFG,若反比例函数y=$\frac{k}{x}$的图象经过点E,则k的值是( )
如图,已知点A(1,0),B(0,2),以AB为边在第一象限内作正方形ABCD,直线CD与y轴交于点G,再以DG为边在第一象限内作正方形DEFG,若反比例函数y=$\frac{k}{x}$的图象经过点E,则k的值是( )
 如图,已知点A(1,0),B(0,2),以AB为边在第一象限内作正方形ABCD,直线CD与y轴交于点G,再以DG为边在第一象限内作正方形DEFG,若反比例函数y=$\frac{k}{x}$的图象经过点E,则k的值是( )
如图,已知点A(1,0),B(0,2),以AB为边在第一象限内作正方形ABCD,直线CD与y轴交于点G,再以DG为边在第一象限内作正方形DEFG,若反比例函数y=$\frac{k}{x}$的图象经过点E,则k的值是( )| A. | 33 | B. | 34 | C. | 35 | D. | 36 |
8.下列根式是最简二次根式的是( )
| A. | $\sqrt{0.2m}$ | B. | $\sqrt{12a-12b}$ | C. | $\sqrt{15}$ | D. | $\sqrt{\frac{a}{2}}$ |
15.在实数:3.141 59,$\root{3}{64}$,1.010 010 001…,4,2.$\stackrel{••}{01}$,2π,$\frac{22}{7}$中,无理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.已知,在河的两岸有A,B两个村庄,河宽为4千米,A、B两村庄的直线距离AB=10千米,A、B两村庄到河岸的距离分别为1千米、3千米,计划在河上修建一座桥MN垂直于两岸,M点为靠近A村庄的河岸上一点,则AM+BN的最小值为( )
| A. | 2$\sqrt{13}$ | B. | 1+3$\sqrt{5}$ | C. | 3+$\sqrt{37}$ | D. | $\sqrt{85}$ |
9.-3的绝对值等于( )
| A. | -3 | B. | -$\frac{1}{3}$ | C. | ±3 | D. | 3 |
 把棱长为a的正方体摆放成 如图的形状,从上向下数,第一层1个,第二层3个,…,按这种规律摆放,第五层的正方体的个数是15.
把棱长为a的正方体摆放成 如图的形状,从上向下数,第一层1个,第二层3个,…,按这种规律摆放,第五层的正方体的个数是15.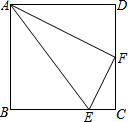 如图,E、F分别是正方形ABCD中BC和CD边上的点,CE=$\frac{1}{4}$BC,F为CD的中点,连接AF、AE、EF,
如图,E、F分别是正方形ABCD中BC和CD边上的点,CE=$\frac{1}{4}$BC,F为CD的中点,连接AF、AE、EF,