题目内容
1.先化简,再求值:((2x+y)2-y(y+4x)-8xy)÷2x,其中x=$\frac{1}{2}$,y=-1.
分析 应用完全平方公式,乘法分配律将原式展开,合并同类项,再做除法运算,最后代值计算即可.
解答 解:[(2x+y)2-y(y+4x)-8xy]÷2x
=[4x2+4xy+y2-y2-4xy-8xy]÷2x
=(4x2-8xy)÷(2x)
=2x-4y,
当x=$\frac{1}{2}$,y=-1时,
原式=2×$\frac{1}{2}$-4×(-1)
=1+4
=5.
点评 本题考查的是整式的混合运算,主要考查了完全平方公式,乘法分配律,多项式除以单项式以及合并同类项的知识点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.将点A(x,1-y)向下平移5个单位长度得到点B(1+y,x),则点(x,y)在平面直角坐标系的( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
5. 如图,在△ABC中,AB=AC,BD平分∠ABC,若∠A=52°,则∠1的度数为( )
如图,在△ABC中,AB=AC,BD平分∠ABC,若∠A=52°,则∠1的度数为( )
 如图,在△ABC中,AB=AC,BD平分∠ABC,若∠A=52°,则∠1的度数为( )
如图,在△ABC中,AB=AC,BD平分∠ABC,若∠A=52°,则∠1的度数为( )| A. | 64° | B. | 78° | C. | 84° | D. | 88° |
12.一个直角三角形的两边长分别为4cm、3cm,则第三条边长为( )
| A. | 5cm | B. | 4cm | C. | $\sqrt{7}$cm | D. | 5cm 或$\sqrt{7}$cm |
10.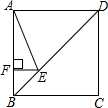 如图,正方形ABCD的边长为8,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )
如图,正方形ABCD的边长为8,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )
 如图,正方形ABCD的边长为8,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )
如图,正方形ABCD的边长为8,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | 8-4$\sqrt{2}$ | D. | 8$\sqrt{2}$-8 |
