题目内容

14．①计算：$\frac{3a+b}{a+2b}$-$\frac{a-3b}{a+2b}$；  
②求值：$\frac{a}{a-1}$-$\frac{1}{a^2-a}$，选取一个你喜欢的a的值代入求值．

分析 ①原式利用同分母分式的减法法则计算即可得到结果；
②原式通分并利用同分母分式的减法法则计算，约分得到最简结果，把a=2代入计算即可求出值．

解答 解：①原式=$\frac{3a+b-a+3b}{a+2b}$=$\frac{2（a+2b）}{a+2b}$=2；
②原式=$\frac{{a}^{2}-1}{a（a-1）}$=$\frac{（a+1）（a-1）}{a（a-1）}$=$\frac{a+1}{a}$，
当a=2时，原式=$\frac{3}{2}$．

点评 此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．

练习册系列答案
相关题目
5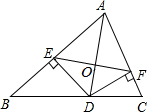．如图，AD是△ABC的角平分线，DE，DF分别是△ABD和△ACD的高，得到下列四个结论：
①OA=OD；
②AD⊥EF；
③当∠A=90°时，四边形AEDF是正方形；
④AE2+DF2=AF2+DE2．
其中正确的是（　　）
A．②③B．②④C．①③④D．②③④
6．已知△ABC∽△DEF，若△ABC与△DEF的相似比为2：3，则△ABC与△DEF对应边上中线的比为2：3．
2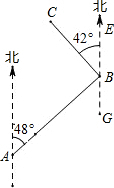．如图，在A、B 两地之间要修一条笔直的公路，从A地测得公路走向是北偏东48°，A，B两地同时开工，若干天后公路准确接通，若公路AB长8千米，另一条公路BC长是6千米，且BC的走向是北偏西42°，则A地到公路BC的距离是（　　）
A．6千米B．8千米C．10千米D．14千米
9．已知x2-5xy+6y2=0，则x：y等于（　　）
A．$\frac{1}{3}$或$\frac{1}{2}$B．2或3C．$\frac{1}{6}$或1D．6或1
19．如图，∠3=∠4，则从下列条件中不能推出AB∥CD的是（　　）
A．∠1与∠2互余B．∠1=∠2C．∠ABC=∠DCBD．BM∥CN
6．根据下面表格中的取值，方程x2+x-3=0有一个根的近似值（精确到0.1）是（　　）
x1.21.31.41.5
x2+x-3-0.36-0.010.360.75
A．1.5B．1.2C．1.3D．1.4
3．分式①$\frac{{x}^{2}+{y}^{2}}{x-y}$+$\frac{2xy}{y-x}$；②$\frac{{x}^{2}-{y}^{2}}{4xy}$-$\frac{{x}^{2}+{y}^{2}}{4xy}$；③$\frac{{a}^{2}}{a-b}$+$\frac{{a}^{2}-a+b}{b-a}$中，计算结果是整式的序号为①③．
4．解方程
（1）8x=2x-6
（2）$\frac{2y-1}{3}=\frac{y+2}{4}-1$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网