题目内容
 如图,Rt△ABC的内切圆⊙O与斜边AB切于点D,与两直角分别切于点E、S,DE与AC的延长线交于点F,请判断BD与CF有何关系?写出你的猜想,并加以证明.
如图,Rt△ABC的内切圆⊙O与斜边AB切于点D,与两直角分别切于点E、S,DE与AC的延长线交于点F,请判断BD与CF有何关系?写出你的猜想,并加以证明.考点:切线的性质
专题:
分析:连接OE、OS、OB,则四边形OECS是正方形,然后证明△OBE≌△EFC,根据全等三角形的对应边相等即可证得.
解答: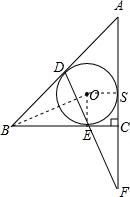 解:BD=CF.
解:BD=CF.
证明:连接OE、OS、OB,则四边形OECS是正方形.
则EC=EO,
∵BA和BC是圆的切线,
∴BD=BE,OB⊥DE,
∴∠BED=∠EOB,
又∵∠BED=∠ECF,
∴∠CEF=∠EOB.
在直角△OBE和直角△EFC中,
,
∴△OBE≌△EFC(ASA),
∴BE=CF.
又∵BD=BE,
∴BD=CF.
 解:BD=CF.
解:BD=CF.证明:连接OE、OS、OB,则四边形OECS是正方形.
则EC=EO,
∵BA和BC是圆的切线,
∴BD=BE,OB⊥DE,
∴∠BED=∠EOB,
又∵∠BED=∠ECF,
∴∠CEF=∠EOB.
在直角△OBE和直角△EFC中,
|
∴△OBE≌△EFC(ASA),
∴BE=CF.
又∵BD=BE,
∴BD=CF.
点评:本题考查了三角形的内切圆,证明△OBE≌△EFC的关键是注意到四边形OECS是正方形.

练习册系列答案
相关题目
已知等腰△ABC的边长为3、5,则腰AC的长可能为( )
| A、5 | B、5或3 | C、3 | D、2 |
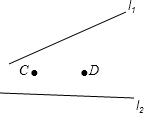 如图,一个人从C点骑马出发到D点,但他必须先到河岸边l1的P1点去让马饮水,然后再到河岸边l2的P2点去,再次让马饮水,最后骑马到D点,他应如何选择饮水点P1,P2.才能使所走的路程CP1+P1P2+P2D最短?
如图,一个人从C点骑马出发到D点,但他必须先到河岸边l1的P1点去让马饮水,然后再到河岸边l2的P2点去,再次让马饮水,最后骑马到D点,他应如何选择饮水点P1,P2.才能使所走的路程CP1+P1P2+P2D最短? 如图所示矩形纸片ABCD,长AD=9cm,宽AB=3cm,将纸片折叠,使点D与点B重合,则DE=
如图所示矩形纸片ABCD,长AD=9cm,宽AB=3cm,将纸片折叠,使点D与点B重合,则DE=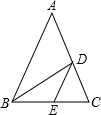 如图,在△ABC中,AB=AC,D、E两点分别在AC、BC上,BD是∠ABC的平分线,DE∥AB,若BE=5cm,CE=3cm,则△CDE的周长是
如图,在△ABC中,AB=AC,D、E两点分别在AC、BC上,BD是∠ABC的平分线,DE∥AB,若BE=5cm,CE=3cm,则△CDE的周长是