题目内容
3.化简:$\frac{3}{x-1}$-$\frac{1}{x+1}$-$\frac{{x}^{2}-3}{1-{x}^{2}}$-1,再从-1,0,1这三个数中选一个合适的数求值.分析 原式通分并利用同分母分式的加减法法则计算,约分得到最简结果,把x=0代入计算即可求出值.
解答 解:$\frac{3}{x-1}$-$\frac{1}{x+1}$-$\frac{{x}^{2}-3}{1-{x}^{2}}$-1
=$\frac{3(x+1)}{(x+1)(x-1)}$-$\frac{x-1}{(x+1)(x-1)}$+$\frac{{x}^{2}-3}{(x+1)(x-1)}$-$\frac{{x}^{2}-1}{(x+1)(x-1)}$
=$\frac{3x+3-x+1+{x}^{2}-3-{x}^{2}+1}{(x+1)(x-1)}$
=$\frac{2(x+1)}{(x+1)(x-1)}$
=$\frac{2}{x-1}$,
当x=0时,原式=$\frac{2}{0-1}$=-2.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
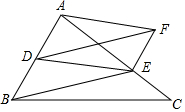 如图,在△ABC中,D是AB边上的中点,E是AC上一点,DF∥BE,EF∥AB,且DF、EF相交于F.
如图,在△ABC中,D是AB边上的中点,E是AC上一点,DF∥BE,EF∥AB,且DF、EF相交于F. 如图,用方向和距离表示火车站相对于仓库的位置是东偏北20°方向,距离仓库50km.
如图,用方向和距离表示火车站相对于仓库的位置是东偏北20°方向,距离仓库50km.
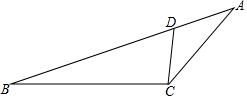 如图,点D在△ABC的AB边上,且∠ACD=∠A.
如图,点D在△ABC的AB边上,且∠ACD=∠A.