题目内容
20.某班有40个同学,同时参加一场数学考试,已知该次考试的平均分为80分,则不及格(小于60分)的学生最多有19个.(注意:所有的分数都是整数)分析 设不及格(小于60分)的学生最多有x人,则及格的人数为(40-x)人,根据及格人数的总分+不及格人数的总分≥40人的总分,建立不等式求出其解即可.
解答 解:设不及格(小于60分)的学生最多有x人,则及格的人数为(40-x)人,由题意,得
100(40-x)+59x≥40×80,
解得:x≤$\frac{800}{41}$.
∵x为整数,
∴x最大为19.
故答案为:19.
点评 本题考查了列一元一次不等式解实际问题的运用,一元一次不等式的解法的运用,解答时解答时根据及格人数的总分+不及格人数的总分≥40人的总分建立不等式是关键.

练习册系列答案
相关题目
12.已知直线y=kx+b,若k+b<0,kb>0,那么该直线不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
9.正八边形的每个外角为( )
| A. | 60° | B. | 45° | C. | 35° | D. | 36° |
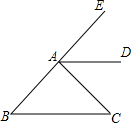 如图,AD是∠EAC的平分线,∠B=∠EAD,求证:∠B=∠C.
如图,AD是∠EAC的平分线,∠B=∠EAD,求证:∠B=∠C.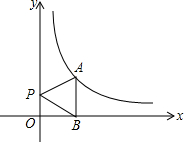 已知点A(m、n)是反比例函数$y=\frac{4}{x}$(x>0)的图象上一点,过A作AB⊥x轴于点B,P是y轴上一点,
已知点A(m、n)是反比例函数$y=\frac{4}{x}$(x>0)的图象上一点,过A作AB⊥x轴于点B,P是y轴上一点,