题目内容
10.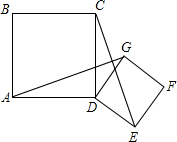 已知:如图,正方形ABCD与正方形DEFG有公共顶点D,联结AG、CE,求证:AG=CE.
已知:如图,正方形ABCD与正方形DEFG有公共顶点D,联结AG、CE,求证:AG=CE.
分析 由四边形ABCD与DEFG是正方形,可得AD=CD,∠ADC=∠GDE=90°,进而得出∠ADG=∠CDE,DG=DE,然后由SAS即可判定△ADG≌△CDE,则可证得AG=CE.
解答 证明:∵ABCD和DEFG是正方形,
∴AD=CD,DG=DE,且∠ADC=∠GDE=90°,
∴∠ADG=∠CDE,
在△ADG与△CDE中,
$\left\{\begin{array}{l}{AD=CD}\\{∠ADG=∠CDE}\\{DG=DE}\end{array}\right.$,
∴△ADG≌△CDE(SAS),
∴AG=CE.
点评 此题考查了全等三角形的判定与性质,关键是由SAS判定△ADG≌△CDE.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
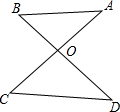 如图,AC,BD相交于点O,∠A=36°,∠B=45°,∠C=48°,则∠D的度数为33°.
如图,AC,BD相交于点O,∠A=36°,∠B=45°,∠C=48°,则∠D的度数为33°. 如图,△ABC中,D是BA延长线上一点,AE平分∠DAC,且AE∥BC,∠B与∠C相等吗?为什么?
如图,△ABC中,D是BA延长线上一点,AE平分∠DAC,且AE∥BC,∠B与∠C相等吗?为什么?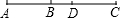 如图,已知线段AB=6延长线段AB到C,使BC=2AB,点D是AC的中点,则BD=3.
如图,已知线段AB=6延长线段AB到C,使BC=2AB,点D是AC的中点,则BD=3.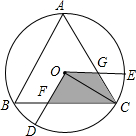 如图,△ABC是⊙O的内接等边三角形,⊙O的半径0D、OE分别交BC、CA于点F、G,∠DOE=120°.探索四边形0FCG的面积(图中阴影部分)与△ABC面积之间的数量关系,并说明理由(提示:连接0B、OC)
如图,△ABC是⊙O的内接等边三角形,⊙O的半径0D、OE分别交BC、CA于点F、G,∠DOE=120°.探索四边形0FCG的面积(图中阴影部分)与△ABC面积之间的数量关系,并说明理由(提示:连接0B、OC)