题目内容
19.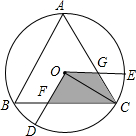 如图,△ABC是⊙O的内接等边三角形,⊙O的半径0D、OE分别交BC、CA于点F、G,∠DOE=120°.探索四边形0FCG的面积(图中阴影部分)与△ABC面积之间的数量关系,并说明理由(提示:连接0B、OC)
如图,△ABC是⊙O的内接等边三角形,⊙O的半径0D、OE分别交BC、CA于点F、G,∠DOE=120°.探索四边形0FCG的面积(图中阴影部分)与△ABC面积之间的数量关系,并说明理由(提示:连接0B、OC)
分析 连接OA,OB,证明△AOC≌△COB≌△BOA,求出∠AOC以及∠DOE之间的关系即可.
解答 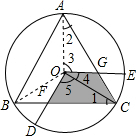 解:S四边形OFCG=$\frac{1}{3}$S△ABC.
解:S四边形OFCG=$\frac{1}{3}$S△ABC.
理由:连接OA,OB和OC,则
∵△ABC是等边三角形,
∴△AOC≌△COB≌△BOA,∠1=∠2;
∴∠AOC=∠3+∠4=120°,∠DOE=∠5+∠4=120°,
∴∠3=∠5.
在△OAG和△OCF中,
$\left\{\begin{array}{l}∠2=∠1\\ OA=OC\\∠3=∠5\end{array}\right.$,
∴△OAG≌△OCF(ASA),
∴S△OAG=S△OCF,
∴S△OAG+S△OGC=S△OCF+S△OGC,即S四边形OFCG=S△OAC=$\frac{1}{3}$S△ABC.
点评 本题考查的是三角形的外接圆与外心,根据题意作出辅助线,构造出全等三角形是解答此题的关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
9.下列代数式中,①-8a3;②xy;③p-1;④0;⑤-$\frac{m+n}{2}$是单项式的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.表一、图1、图2是根据某初中学校2000名学生为四川雅安灾区捐款的情况而制作的统计图表.
(1)请你将表一、图1补充完整.
(2)该校九年级有660名学生.
(3)八年级的学生小明看了表一说:“我们八年级捐款最多,因此我们八年级学生最有爱心”.你认为小明的说法对吗?简单说说你的理由.
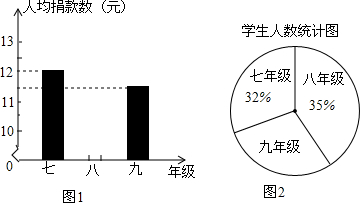
(1)请你将表一、图1补充完整.
| 年级 | 七年级 | 八年级 | 九年级 |
| 捐款(元) | 7680 | 7700 | 7590 |
(3)八年级的学生小明看了表一说:“我们八年级捐款最多,因此我们八年级学生最有爱心”.你认为小明的说法对吗?简单说说你的理由.

11.在△ABC和△DEF中,按照下列给出的条件,能用“SAS”公理判定△ABC≌△DEF的是( )
| A. | AB=DE,∠A=∠D,BC=EF | B. | AB=EF,∠A=∠D,AC=DF | ||
| C. | AB=BC,∠B=∠E,DE=EF | D. | BC=EF,∠C=∠F,AC=DF |
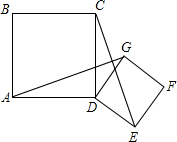 已知:如图,正方形ABCD与正方形DEFG有公共顶点D,联结AG、CE,求证:AG=CE.
已知:如图,正方形ABCD与正方形DEFG有公共顶点D,联结AG、CE,求证:AG=CE.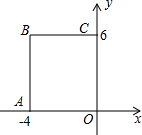 如图,在平面直角坐标系中,矩形OABC的顶点O在坐标原点,A(-4,0),C(0,6),如果矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的$\frac{1}{4}$,那么点B的对应点B′的坐标是(-2,3)或(2,-3).
如图,在平面直角坐标系中,矩形OABC的顶点O在坐标原点,A(-4,0),C(0,6),如果矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的$\frac{1}{4}$,那么点B的对应点B′的坐标是(-2,3)或(2,-3).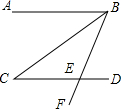 如图,已知AB∥CD,BC平分∠ABE,∠C=35°,则∠CEF的度数是70°.
如图,已知AB∥CD,BC平分∠ABE,∠C=35°,则∠CEF的度数是70°.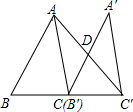 已知:如图,△ABC的面积为12,将△ABC沿BC方向移到△A′B′C′的位置,使B′与C重合,连结AC′交A′C于D,则△C′DC的面积为6.
已知:如图,△ABC的面积为12,将△ABC沿BC方向移到△A′B′C′的位置,使B′与C重合,连结AC′交A′C于D,则△C′DC的面积为6.