题目内容
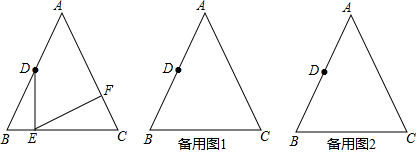
18.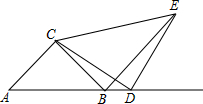 如图,已知△ABC,CA=CB,DC=DE,∠BCA=∠CDE=90°,D是AB延长线上一点.
如图,已知△ABC,CA=CB,DC=DE,∠BCA=∠CDE=90°,D是AB延长线上一点.(1)求证:CB⊥EB;
(2)求证:2AD-AB=$\sqrt{2}$EB;
(3)若CE=2,AC=$\sqrt{2}$,点F与点D关于CE对称,连BF,则S△EBF=1.
分析 (1)如图1,过C作CG⊥AB于G,过E作EH⊥AB于H,根据全等三角形的性质得到DG=EH,CG=DH,等量代换得到DG=BH=EH,根据平角的定义即可得到结论;
(2)根据等腰直角三角形的性质即可得到结论;
(3)如图2,过B作BH⊥CE于H,连接DF交CE于O,根据对称的性质得到CE⊥DF,OF=OD=$\frac{1}{2}$CE=1,推出△CBE是等腰直角三角形,得到B,D重合,根据三角形的面积即可得到结论;
解答 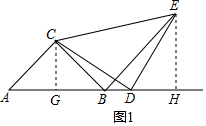 (1)证明:如图1,过C作CG⊥AB于G,过E作EH⊥AB于H,
(1)证明:如图1,过C作CG⊥AB于G,过E作EH⊥AB于H,
∵∠BCA=∠CDE=90°,
∴∠CDG+∠EDH=∠EDH+∠DEH,
∴∠CDG=∠DEH,
在△CDG与△DEH中,$\left\{\begin{array}{l}{∠CGD=∠EHD}\\{∠CDG=∠DEH}\\{CD=DE}\end{array}\right.$,
∴△CDG≌△DEH,
∴DG=EH,CG=DH,
∵CG=BG,
∴DH=BG,
∴DG=BH=EH,
∴∠EBH=45°,
∵∠ABC=45°,
∴∠CBE=90°,
∴CB⊥=BE;
(2)证明:∵2AD-AB=2(AG+DG)-2BG=2(DH+BH)-2DH=2BH,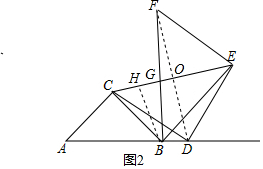
∵BH=$\frac{\sqrt{2}}{2}$BE,
∴2AD-AB=$\sqrt{2}$EB;
(3)如图2,过B作BH⊥CE于H,连接DF交CE于O,
设CE,BF交于点G,
∵点F与点D关于CE对称,
∴CE⊥DF,OF=OD=$\frac{1}{2}$CE=1,
∴OC=OE=$\frac{1}{2}$CE=1,
∵AC=$\sqrt{2}$,
∴BC=$\sqrt{2}$,
∴BE=$\sqrt{2}$,
∴BC=BE,
∴△CBE是等腰直角三角形,
∴B,D重合,
∴S△BEF=S△DEF=$\frac{1}{2}$×2×1=1.
故答案为:1.
点评 本题考查了全等三角形的判定和性质,等腰直角三角形的性质,三角形的面积的求法,正确的作出辅助线是解题的关键.

| A. | 5,6,7 | B. | 0.7,2.4,2.5 | C. | 1,1,2 | D. | 1,$\sqrt{2}$,3 |
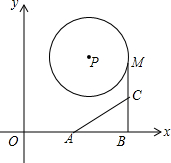 如图,点P(3,4),⊙P半径为2,A(2.8,0),B(5.6,0),点M是⊙P上的动点,点C是MB的中点,则AC的最小值是$\frac{3}{2}$.
如图,点P(3,4),⊙P半径为2,A(2.8,0),B(5.6,0),点M是⊙P上的动点,点C是MB的中点,则AC的最小值是$\frac{3}{2}$.