题目内容
3.已知:二次函数y=-x2+2(α+1)x+1,其中a为常数.(1)若y的最大值为2,求a的值;
(2)求y=-x2+2(a+1)x+1在0≤x≤|a|时的最小值;
(3)若方程|-x2+2(a+1)x+1|=2-x的正实数根只有一个,求a的取值范围.
分析 (1)把y=-x2+2(α+1)x+1配方即可得到结论;
(2)根据二次函数的性质即可得到结论;
(3根据题意得到即该方程的一次项的系数为0,判别式△≥0且二次项的系数与常数项的符号相反.解方程即可得到结论.
解答 解:(1)∵二次函数y=-x2+2(α+1)x+1=-[x-(a+1)]2+a2+2a+2,
∵y的最大值为2,
∴a2+2a+2=2
解得:a=0或a=-2
即y的最大值为2时,a的值为0或-2;
(2)∵二次函数y=-x2+2(α+1)x+1=-[x-(a+1)]2+(a+1)2+1的图象开口向下,对称轴x=a+1
∴当0≤x≤|a|时,函数值随x的增大而增大,
故:函数y=-x2+2(a+1)x+1的最小值为:ymin═-[0-(a+1)]2+(a+1)2+1=1;
(3)∵方程|-x2+2(a+1)x+1|=2-x的正实数根只有一个,即该方程的一次项的系数为0,判别式△≥0且二次项的系数与常数项的符号相反.
∴当方程-x2+2(a+1)x+1=2-x时,
有:x2-(2a+3)x+1=0,而此时二次项的系数与常数项的符号相同,不符合题意,舍去.
∴当方程为:-x2+2(a+1)x+1=x-2时,化简整理得:x2-(2a+1)x-3=0,
∵△=[-(2a+1)]2-4×(-3)=4a2+4a+13=(2a+1)2+12≥0,
∴a的取值范围为任意实数.
点评 本题考查了二次函数的最值,二次方程的判别式,正确的理解题意是解题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
7.实验:袋中装有8个黑球,4个白球,这些球的形状、大小、质地等完全相同,在看不到的条件下,随机地从袋子中摸出1个球.
我们把“摸到黑球”记为事件A,吧“摸到白球”记为事件B,填写下表并回答问题.
(1)事件A和事件B是随机事件吗?
(2)哪个事件发生的可能性大?
(3)你认为“10次摸球”和“20次摸球”哪种实验更能获得较正确的结论?
(4)为了尽可能获得正确结论,我们应该怎样做?
我们把“摸到黑球”记为事件A,吧“摸到白球”记为事件B,填写下表并回答问题.
| 事件A发生的次数 | 事件B发生的次数 | 结果(指哪个事件发生的次数多) | |
| 10次摸球 | |||
| 20次摸球 |
(2)哪个事件发生的可能性大?
(3)你认为“10次摸球”和“20次摸球”哪种实验更能获得较正确的结论?
(4)为了尽可能获得正确结论,我们应该怎样做?
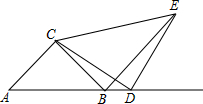 如图,已知△ABC,CA=CB,DC=DE,∠BCA=∠CDE=90°,D是AB延长线上一点.
如图,已知△ABC,CA=CB,DC=DE,∠BCA=∠CDE=90°,D是AB延长线上一点. 如图,△ABC中,AB=AC,点D是边AB上一点,且AD:DB=1:2,cot∠DCB=$\sqrt{2}$,CD=4$\sqrt{3}$.
如图,△ABC中,AB=AC,点D是边AB上一点,且AD:DB=1:2,cot∠DCB=$\sqrt{2}$,CD=4$\sqrt{3}$.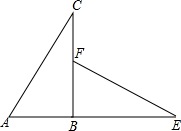 如图,△ABC是直角三角形,延长AB到点E,使BE=BC,在BC上取一点F,使BF=AB,连接EF,△ABC旋转后能与△FBE重合,请回答:
如图,△ABC是直角三角形,延长AB到点E,使BE=BC,在BC上取一点F,使BF=AB,连接EF,△ABC旋转后能与△FBE重合,请回答: