题目内容
已知△ABC和△A′B′C′中，∠B=25°，∠C=50°，∠B′=105°，∠C′=25°，这两个三角形相似吗？
考点：相似三角形的判定
专题：
分析：先根据三角形内角和定理求出∠A及∠A′的值，进而可得出结论．
解答：解：相似．
理由：在△ABC中，
∵∠B=25°，∠C=50°，
∴∠A=180°-25°-50°=105°；
在△A′B′C′中，
∵∠B′=105°，∠C′=25°，
∴∠A′=180°-105°-25°=50°，
∴∠B=∠C′，∠C=∠A′，
∴△ABC∽△B′C′A′．
理由：在△ABC中，
∵∠B=25°，∠C=50°，
∴∠A=180°-25°-50°=105°；
在△A′B′C′中，
∵∠B′=105°，∠C′=25°，
∴∠A′=180°-105°-25°=50°，
∴∠B=∠C′，∠C=∠A′，
∴△ABC∽△B′C′A′．
点评：本题考查的是相似三角形的判定，熟知有两组角对应相等的两个三角形相似是解答此题的关键．
练习册系列答案
相关题目
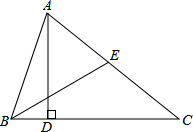在△ABC中，AD⊥BC于D点，BE为中线，且∠CBE=30°．求证：AD=BE．