题目内容
如图所示:
(1)求图甲中∠A+∠B+∠C+∠D+∠E的度数;
(2)如图乙,如果点E向左移动到AD上,计算∠A+∠B+∠C+∠D+∠BEC的度数;
(3)如图丙,当点E移到AD的另一侧时,直接写出∠A+∠B+∠C+∠D+∠E的值;
(4)如图丁,∠A+∠B+∠C+∠D+∠E的大小有变化吗?说明理由.
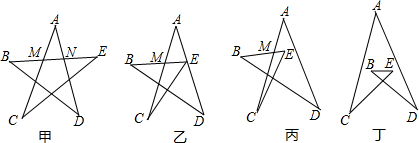
(1)求图甲中∠A+∠B+∠C+∠D+∠E的度数;
(2)如图乙,如果点E向左移动到AD上,计算∠A+∠B+∠C+∠D+∠BEC的度数;
(3)如图丙,当点E移到AD的另一侧时,直接写出∠A+∠B+∠C+∠D+∠E的值;
(4)如图丁,∠A+∠B+∠C+∠D+∠E的大小有变化吗?说明理由.

考点:三角形内角和定理,三角形的外角性质
专题:
分析:(1)先根据三角形外角的性质得出∠C+∠E=∠AMN,∠B+∠D=∠ANM,再由三角形内角和定理即可得出结论;
(2)先根据三角形外角的性质得出∠C+∠BEC=∠AME,∠B+∠D=∠AEM,再由三角形内角和定理即可得出结论;
(3)延长BE交AD于点N,再根据三角形外角的性质得出∠C+∠BEC=∠AMN,∠B+∠D=∠ANM,再由三角形内角和定理即可得出结论;
(4)延长BE交AD于F,根据三角形外角的性质可得出结论.
(2)先根据三角形外角的性质得出∠C+∠BEC=∠AME,∠B+∠D=∠AEM,再由三角形内角和定理即可得出结论;
(3)延长BE交AD于点N,再根据三角形外角的性质得出∠C+∠BEC=∠AMN,∠B+∠D=∠ANM,再由三角形内角和定理即可得出结论;
(4)延长BE交AD于F,根据三角形外角的性质可得出结论.
解答: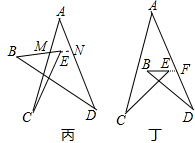 解:(1)如图甲,
解:(1)如图甲,
∵∠AMN是△CEM的外角,
∴∠C+∠E=∠AMN.
∵∠ANM是△BDN的外角,
∴∠B+∠D=∠ANM.
∵∠A+∠AMN+∠ANM=180°,
∴∠A+∠B+∠C+∠D+∠E=180°;
(2)如图丙,
∵∠AME是△CEM的外角,
∴∠C+∠BEC=∠AME.
∵∠AEM是△BDE的外角,
∴∠B+∠D=∠AEM.
∵∠A+∠AME+∠AEM=180°,
∴∠A+∠B+∠C+∠D+∠BEC=180°;
(3)如图丙,延长BE交AD于点N,
∵∠AMN是△CEM的外角,
∴∠C+∠BEC=∠AMN.
∵∠ANM是△BDN的外角,
∴∠B+∠D=∠ANM,
∵∠A+∠AMN+∠ANM=180°,
∴∠A+∠B+∠C+∠D+∠E=180°;
(4)如图丁,延长BE交AD于F,
∵∠EFD+∠D+∠EGD=180°,
∴∠A+∠C+∠B+∠E+∠D=180°.
 解:(1)如图甲,
解:(1)如图甲,∵∠AMN是△CEM的外角,
∴∠C+∠E=∠AMN.
∵∠ANM是△BDN的外角,
∴∠B+∠D=∠ANM.
∵∠A+∠AMN+∠ANM=180°,
∴∠A+∠B+∠C+∠D+∠E=180°;
(2)如图丙,
∵∠AME是△CEM的外角,
∴∠C+∠BEC=∠AME.
∵∠AEM是△BDE的外角,
∴∠B+∠D=∠AEM.
∵∠A+∠AME+∠AEM=180°,
∴∠A+∠B+∠C+∠D+∠BEC=180°;
(3)如图丙,延长BE交AD于点N,
∵∠AMN是△CEM的外角,
∴∠C+∠BEC=∠AMN.
∵∠ANM是△BDN的外角,
∴∠B+∠D=∠ANM,
∵∠A+∠AMN+∠ANM=180°,
∴∠A+∠B+∠C+∠D+∠E=180°;
(4)如图丁,延长BE交AD于F,
∵∠EFD+∠D+∠EGD=180°,
∴∠A+∠C+∠B+∠E+∠D=180°.
点评:本题考查的是三角形内角和定理及三角形内角与外角的关系,解答此类题目时利用三角形内角与外角的关系把多个角划到同一个三角形中,再利用三角形内角和定理解答即可.

练习册系列答案
相关题目
 如图,在△ABC中,AC=BC=3,AB=3
如图,在△ABC中,AC=BC=3,AB=3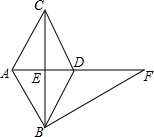 如图,BC垂直平分AD,垂足为E,AD平分∠BAC
如图,BC垂直平分AD,垂足为E,AD平分∠BAC 如图,AD平分∠BAC,∠D=∠DAB,E在AD上,BE的延长线交CD于F,连CE,且∠1=∠2,试说明AB=AC.
如图,AD平分∠BAC,∠D=∠DAB,E在AD上,BE的延长线交CD于F,连CE,且∠1=∠2,试说明AB=AC.