题目内容
已知,△ABC∽△DEF,BG、EH分别是△ABC和△DEF的角平分线,BC=6cm,EF=4cm,BG=4.8cm.求EH的长.
考点:相似三角形的性质
专题:
分析:直接利用相似三角形的性质,相似三角形对角线的比等于相似比,求出即可.
解答: 解:如图所示:
解:如图所示:
∵△ABC∽△DEF,
∴
=
,
即
=
,
解得:EH=2.4.
 解:如图所示:
解:如图所示:∵△ABC∽△DEF,
∴
| BG |
| EH |
| BC |
| EF |
即
| 4.8 |
| EH |
| 6 |
| 4 |
解得:EH=2.4.
点评:此题主要考查了相似三角形的性质,正确应用相似三角形的性质是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若分解因式a2+ma+
=(a-
)2,则m等于( )
| 1 |
| 4 |
| 1 |
| 2 |
| A、-2 | B、2 | C、1 | D、-1 |
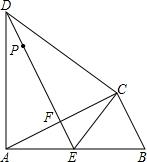 如图,在△ABC中,∠ACB=90°,以AC为底边作等腰△ACD,AD=CD,E是AB的中点,连接CE、DE,DE与AC相交于点F.求证:DE∥BC.
如图,在△ABC中,∠ACB=90°,以AC为底边作等腰△ACD,AD=CD,E是AB的中点,连接CE、DE,DE与AC相交于点F.求证:DE∥BC.